Jicong Fan 교수방에서 나온 논문이고 (논문링크) AAAI25에 accept되었다. related work 조사를 안하는건지 아니면 못본척 하는건지 TabAD SOTA 논문들과 비교를 안하고 있다. 또 용어도 최근에 다시 정립된 용어를 쓰지 않고....ㅠㅠㅠ 옛날에 써둔걸 제출한건가 싶다. (TabAD에서는 normal만 train하는 setting을 최근 semi-supervised라 부르고 있는데 unsupervised AD로 부른다던가...) 하지만 idea자체는 명료하고 말이 된다. 앞선 포스팅에서의 PReNet은 real anomaly를 활용하여 normal과 anomaly와의 점수차를 학습하였다면, 해당 논문은 real anomaly 없이 noise를 추가한 샘플이 hard anomaly와 가깝다는 가정으로 noise를 점차 추가하면서 noise의 정도를 예측하는 regression task를 푼다. 그렇게 했을 때, normal에서 멀어지는 샘플과의 점수차를 gradual하게 학습할 수 있다.
Introduction
Table data는 다양한 분야에서 중요한 data type이고 여기서 anomaly detection을 잘하는 것은 중요하다. 하지만 기존 연구들의 경우 대표적으로 reconstruction based method같은 간접 지표는 일반화나 신뢰성이 부족하다는 한계가 있다. 본 연구는 직접적으로 anomaly score를 학습하는 방식으로 이를 해결한다.
저자는 anomaly 중에서도 hard anomaly 는 normal과 매우 유사한 특징을 가지고 있기 때문에, 이러한 이상 데이터는 정상 데이터가 일정하게 변형(perturbed)된 샘플들로 볼 수도 있다고 가정하고 다양한 perturbated sample을 생성하면 hard anomaly를 생성할 수 있다고 봤다. 모델이 이러한 hard anomaly가 얼마나 perturbed되었는지를 인식할 수 있다면 비교적 쉬운 anomaly까지 탐지할 수 있다. 본 연구는 normal 패턴과 다양한 noise 패턴을 동시에 학습하여, 효과적인 이상 탐지 경계를 구축하고, 미지의 데이터에도 일반화될 수 있는 AD 모델을 제안 한다.
Related works
기존의 오토인코더 기반 방법들이 재구성 오류를 최소화하여 노이즈를 제거 하는 데 집중하는 반면, 제안하는 방법은 노이즈 수준을 직접 평가 하는 점에서 노이즈 제거(diffusion model) 와 유사한 접근 방식을 가진다.
Proposed method
Anomalous Data Decomposition

Detect이 어려운 hard anomaly (D_H)는 easy anomaly (D_E)에 비해 normal에 가깝기 때문에, anomaly는 사실상 normal의 변형(perturbed samples)일 가능성이 높다 는 가설을 세울 수 있다.



따라서, 우리는 normal dataset X에 다양한 노이즈를 추가하여 새로운 데이터셋을 생성할 수 있다.

저자는 noise의 다양성이 충분하다면, noised normal이 hard anomaly pattern을 많이 포함할 것이라고 보고 그렇지 않더라도 두 분포의distance가 충분히 가깝다면 hard anomaly detection에 효과적이라고 설명한다.

Noise Evaluation Model

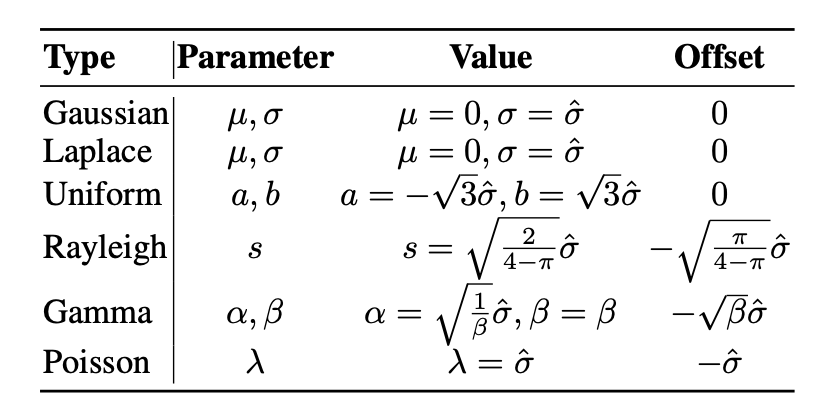
Noisy dataset을 생성하기 위해 training sample의 각 element에 random noise를 더해준다. 이 operation은 data의 quality를 낮춘다. noise level에 따라 k개의 dataset을 union하여 noisy data로 사용한다.

riginal sample이 모델(anomaly scoring function) h를 통과했을 때는 d-dimension vector 0로 수렴하도록, noise가 추가된 샘플이 h를 통과했을 때는 noise level을 맞추도록 학습한다. 이렇게 했을 때, corruption정도를 학습하기 때문에 Binary discrimination 학습보다 더 세밀한 decision boundary를 얻을 수 있다.

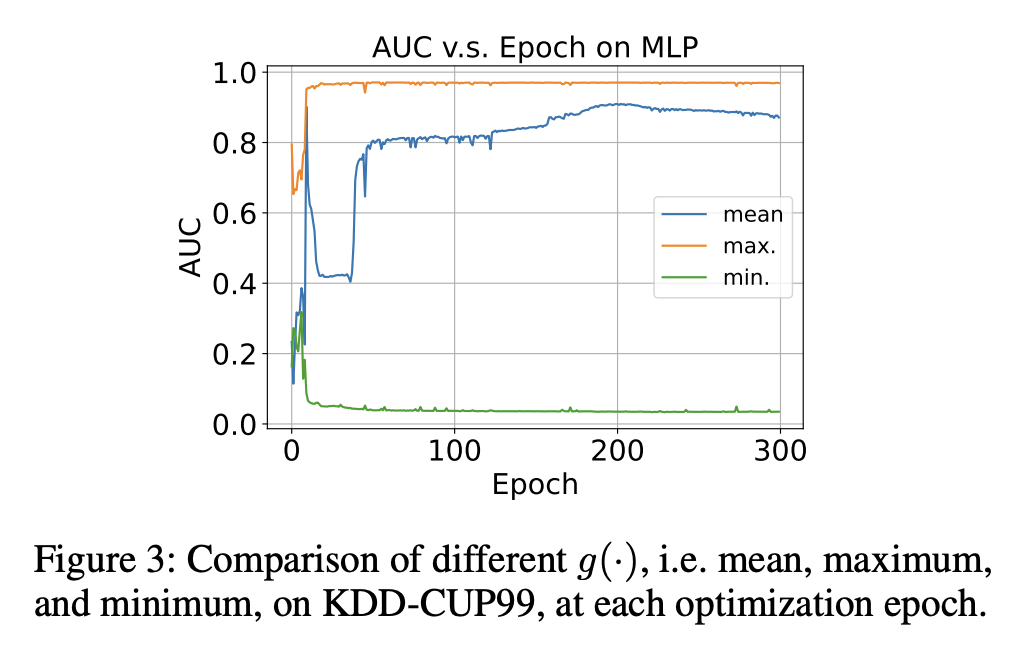
Model output은 column 갯수 d만큼 존재하기 때문에 하나의 anomaly score로 aggreate하기 위한 Layer g를 통과하여 최종 anomaly score를 구하게 된다. g는 maximum, minimum, mean, median or combination이 될 수있다. (각 column dimension별로 anomaly score가 나오기 때문에, Interpretability로도 연결될 수 있다.)

Noise Generation and Model Training
실제로 batch단위로 좀더 자세히 noise 생성에 대해 설명한다. 아래는 noise 생성 알고리즘이다. 핵심만 말하자면, 다양한 크기의 noise를 각 column에 random으로 적용하여 일정한 패턴의 noise에 overfitting되는 것을 막았다. 그리고 noise를 학습하지 않기 때문에 별도의 time cost가 들지 않는 장점이 있다.

Experiments
Main results
두가지 common한 setting에서 평가했다 : Unsupervised anomaly detection, One-class classification
Unsupervised anomaly detection vs One-class classification
- Unsupervised anomaly detection: Normal(0), Abnormal(1)인 data에서 normal만 학습 진행
- One-class classification: 여러 class가 있는 data에서 one-vs-all로 학습 진행
✅ VanillaMLP(4층 MLP)와 ResMLP 두 가지 모델 사용
✅ 가우시안 노이즈 적용, 최대 노이즈 수준 σmax=2\sigma_{max} = 2, 서로 다른 3개의 노이즈 분포 사용
✅ 각 샘플당 3개의 노이즈 변형 데이터 생성 (노이즈 비율: 0.5, 0.8, 1.0)
✅500 epoch 학습, 100번째 epoch에서 학습률 0.1배 감소
✅ g는 maximum을 이용했을 때, 수렴도 제일 빠르고 성능도 제일 좋았다.
✅ 성능은 AUROC와 threshold를 고정했을 때, F1 score를 측정했다.
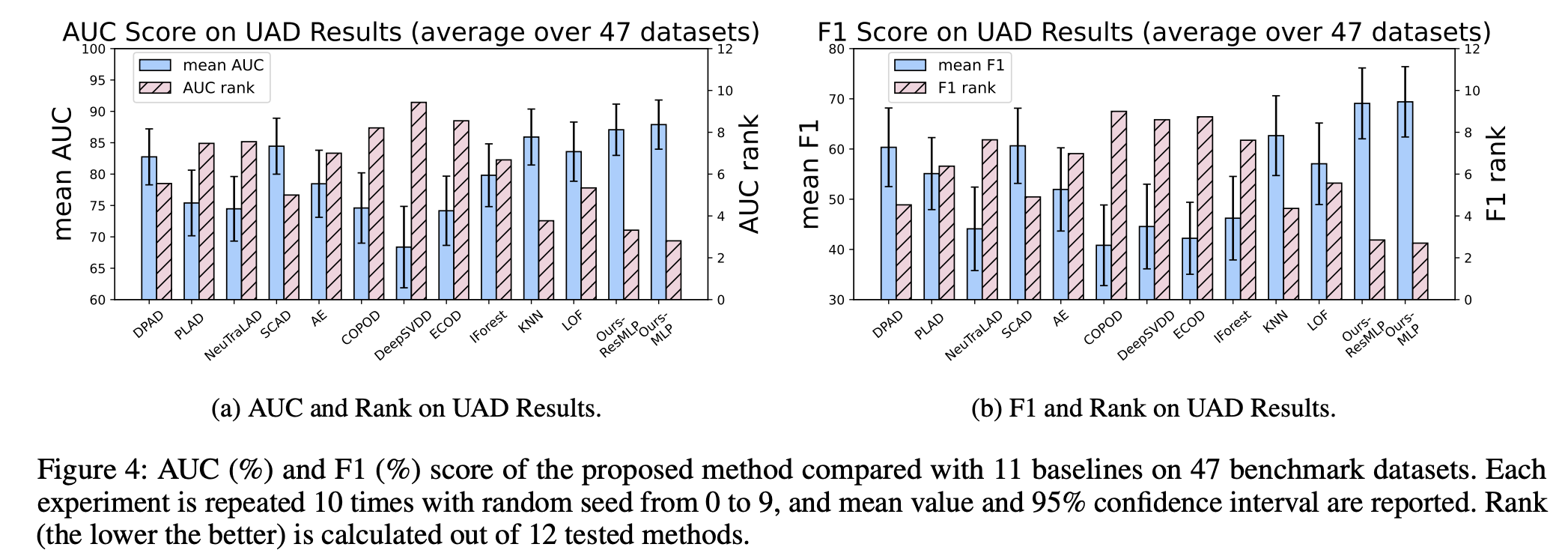
Unsupervised anomaly detection (UAD)
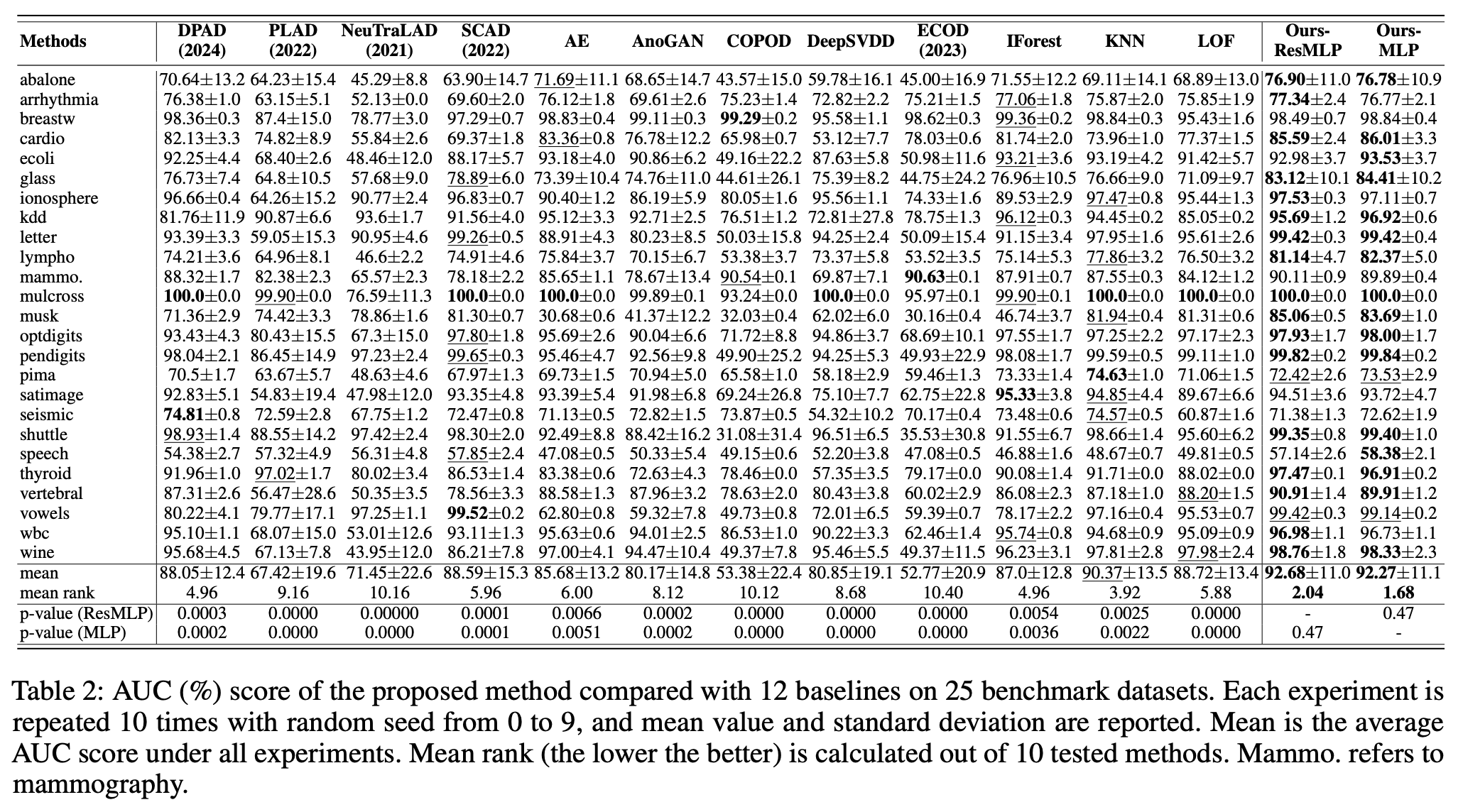
One-class classification
Ablation study
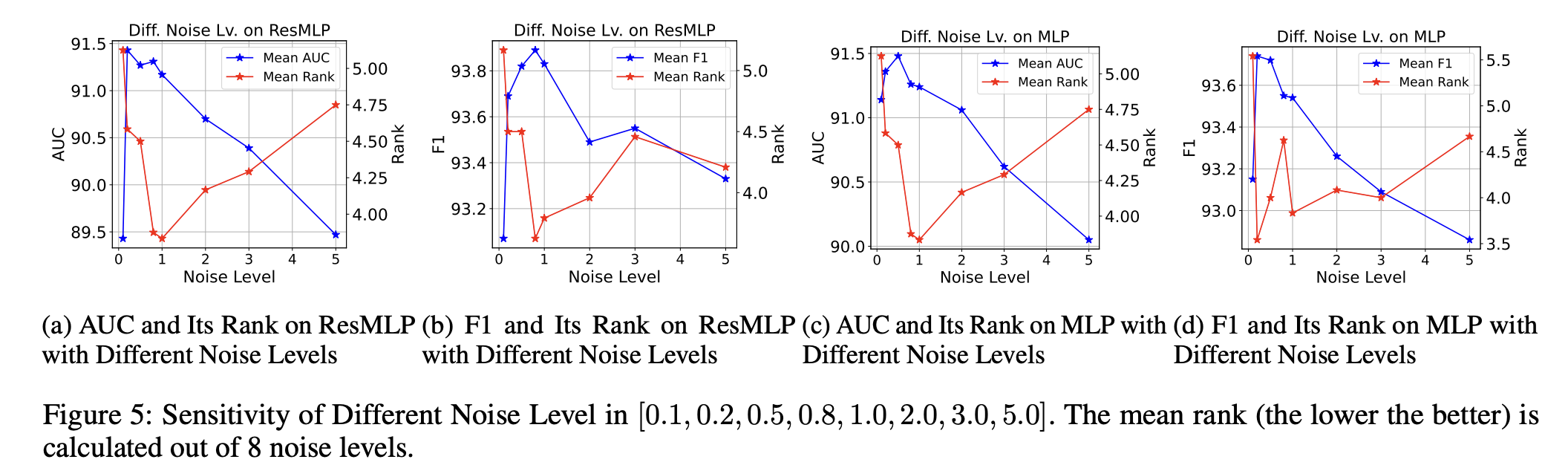
Sensitivity of Different Noise Levels
실험 결과, 노이즈 수준이 너무 작으면 정상 샘플과 이상 샘플 간의 거리가 최소화되어 모델이 혼란스러워진다. 반면, 노이즈 수준이 너무 크면 출력 값의 범위와 샘플링 공간이 확장되어 모델의 효과성이 감소한다. 따라서, 최적의 노이즈 수준은 약 1.0 이다.
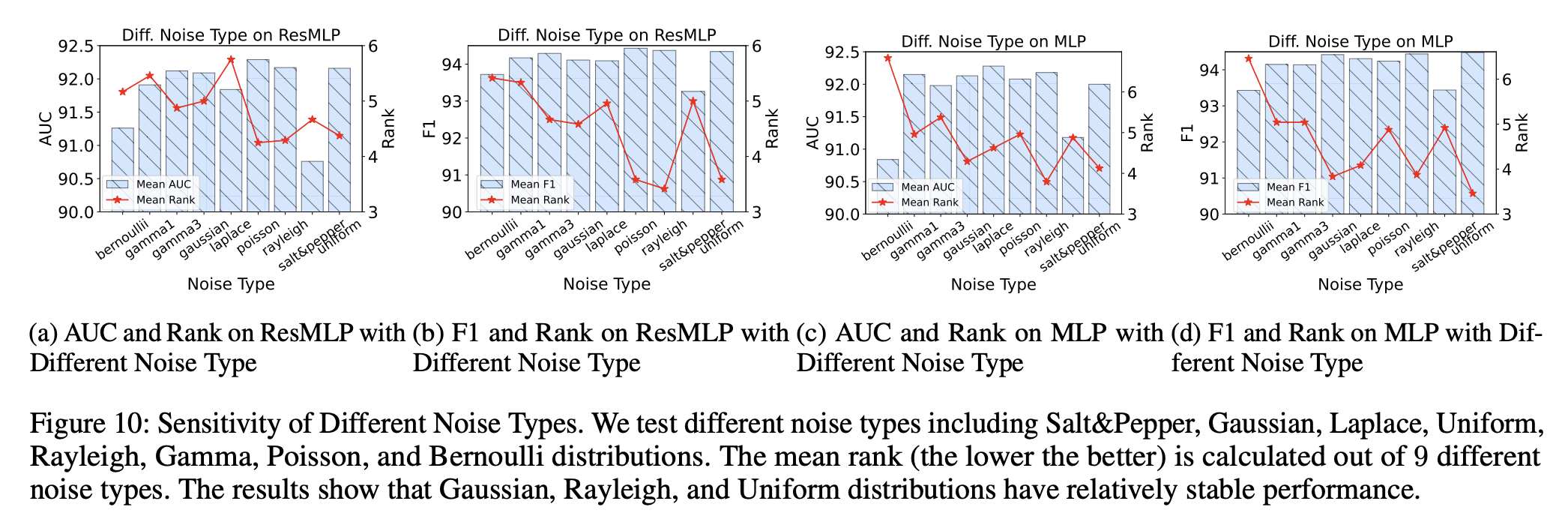
Sensitivity of Different Noise Types
- Salt & Pepper 노이즈와 Bernoulli 노이즈의 성능이 낮음 → 이는 제안된 노이즈 생성 방식이 효과적임을 시사.
- Gaussian, Rayleigh, Uniform 노이즈는 안정적인 성능을 유지:
- AUC 92%, F1-score 94%
- 이는 제안된 방법이 다양한 노이즈 유형에서도 강건함(Robustness)을 유지함을 의미.
Qualitative Visualization
Noisy sample이 real anomaly보다 더 Normal에 가깝게 위치하고 실제로 도움이 되었음을 embedding space에서 알 수 있다.

Conclusion
본 연구에서는 noise evaluation-based unsupervised anomaly detection 방법을 제안하여, 정상 데이터에 노이즈를 추가하여 모델이 이상 패턴을 학습하도록 유도 하였다. 노이즈 크기 예측을 통해 이상치의 정도와 위치를 파악할 수 있으며, 제안한 방법의 일반화 가능성과 신뢰성을 이론적으로 증명 하였다. 47개(UAD) 및 25개(OCC) 실제 테이블 데이터셋에서 기존 기법보다 우수한 성능을 보였으며, Gaussian, Rayleigh, Uniform 노이즈가 안정적인 성능을 유지함을 확인하였다.
'Review > Reading' 카테고리의 다른 글
| Deep Weakly-supervised Anomaly Detection 논문 리뷰 (0) | 2025.03.04 |
|---|---|
| DRL: DECOMPOSED REPRESENTATION LEARNING FOR TABULAR ANOMALY DETECTION 논문 리뷰 (2) | 2025.02.10 |
| Self-supervised learning (자기지도학습)과 Contrastive learning (대조학습): 개념과 방법론 톺아보기 (6) | 2022.02.17 |
| Semi-supervised learning (준지도학습): 개념과 방법론 톺아보기 (6) | 2021.09.09 |
| Glow: Generative Flow with Invertible 1X1 convolutions 논문 리뷰 (2) | 2020.06.14 |



