
DSP를 공부해본 사람이라면 DFT(Discrete Fourier Transform)에 대해 들어본 적이 있을 것이다. DFT는 무엇인가? DTFT와 무엇이 다른가? 여러 궁금증에 앞서 DFT를 이해하기에 앞서 일단 식부터 살펴보고 시작하겠다.

x[n]이라는 유한한 길이의 음성신호가 존재할 때, 각주파수(오메가)를 N개로 쪼갠 후 k번째 주파수에 해당하는 변환 값을 찾아내는 것이 DFT결과가 된다. 식을 먼저 소개했고, 자세한 내용은 아래의 설명들을 통해 차근차근 알아보도록하자.
왜 DFT를 하는가?
컴퓨터는 이산적인 값만 처리가 가능하다. 연속시간신호는 시간축(x축)에서 연속적이기 때문에 샘플링을 하여 이산시간 신호를 만들어야한다. 이와 같은 논리로, 이산시간신호에 대한 주파수변환인 DTFT결과를 확인하면, 변환을 통해 x축이 주파수가 되고 y축은 그 주파수성분에 해당하는 값이 나오게 되는데, 이산시간 비주기신호에 대하여 DTFT를 수행한 결과는 연속주기의 형태로 나오게 된다.(*아래의 표 참고, Duality성질) 그러므로 DTFT결과는 주파수축에서 연속적이기 때문에 컴퓨터에서 처리할 수 없다. 결론적으로는 이산시간신호를 주파수변환하는 DTFT는 컴퓨터에서 쓸 수 없다. 그래서 연속적으로 존재하는 주파수를 쪼개서 이산적으로 만들어야할 필요가 생겼다. 대체할 수 있는 방법으로 나온 것이 DFT이고 이는 DTFT의 주파수샘플링 된 형태가 된다. 정리하면, 시간축에서의 샘플링처럼 DFT를 통해서 주파수축에서 샘플링하여 컴퓨터가 푸리에변환을 처리할 수 있게 하는 것이다.

DTFT를 샘플링하면 DFT이다.

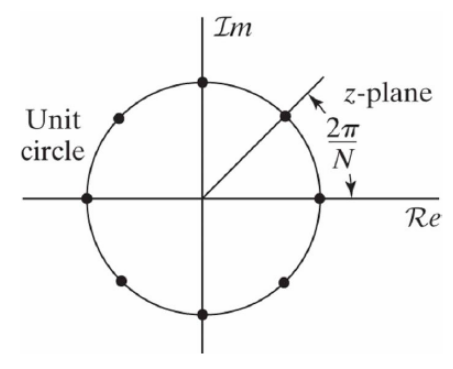
앞서 말했던 것처럼 DTFT에서 주파수를 샘플링한 것이 DFT라고 했다. 주파수축을 샘플링하여 이산 주파수가 된다면 반대로 시간축에서는 주기성을 띄게 된다. DTFT식과 DFT식을 비교하면 쉽게 알 수 있고 그림으로 표현하면 아래와 같다.

sampling theorem을 배웠을 때 주파수축에서 일어나는 aliasing을 방지하기 위한 조건들을 배웠던 것을 상기시켜보면, 두 가지 조건을 만족해야 했다. 1)Band-limited 되어있어야 한다. 2)샘플링 주파수가 신호의 최대 주파수의 2배 이상이 되어야 한다.(Fs≥2Fmax) 이와 유사하게 주파수축에서의 샘플링도 시간축에서 일어나는 aliasing을 방지하기 위한 조건이 필요하다.
- Time-limited 되어 있어야 한다.
- DFT의 sampling rate인 N-point가 신호의 길이(L)보다 크거나 같아야 한다.(N>=L)
시간축에서 주기성을 띄게 된다는 뜻은 주파수샘플링으로 인해 시간축에서 time-aliasing이 생길 수도 있다는 것을 의미한다. 그래서 time-limited 즉, 시간축에서 이산비주기신호가 finite sequence여야만 DFT를 할 수 있다. 이는 아까 살펴본 주파수샘플링 조건 첫번째에 해당하는 설명이 된다. 또한 N-point로 샘플링 하였을 때, 시간축에서는 주기 N으로 주기화되는 것을 확인할 수 있다. 그러므로 신호의 길이 L 보다 N이 더 크거나 같아야 시간상에서 겹치지 않게 된다.주파수축에서의 샘플링도 샘플링이다. 주파수를 더 세심하게 표현(frequency resolution)하기 위해서 N은 클수록 좋다. 이를 구현하기 위해 zero-padding으로 쓸모없는 0을 추가하는 작업을 할 수도 있다.
DFS와 DFT의 결과가 같다. (0≤k≤N-1)
다른 한편으로 봤을 때, 주파수샘플링은 결국 시간축에서 주기화를 유발한다는 점에서 이산 주기신호의 DTFS와 일맥상통하는 내용이다. 여기서 앞에 붙는 scaling값이 N배 차이나기 때문에 DFS를 새로 정의하였고 DFS의 inverse를 취했을 때 나오는 주기신호의 한주기만 취하면 DFS와 DFT식이 같아진다.
DFT의 특성: Circular convolution

LTI시스템에서는 시스템의 output을 input과 시스템의 impulse response의 convolution으로 구한다는 것을 알고있다. 이를 DTFT했을 때는 output을 input과 시스템의 frequency response의 곱으로 나타낼 수 있다. 또한 반대로 둘의 곱을 inverse DTFT를 통해서 convolution으로 나타낼 수 있다. 하지만, DFT의 경우 주파수상에서의 곱을 시간상에서의 convolution으로 표현할 수 없다. 우리가 컴퓨터에서 DFT를 쓰긴 하지만 결론적으로 원하는 것은 Linear convolution이다. 그러므로 왜 Circular convolution이 발생하는 지 알아보고, 직접 예시를 통해 계산해본 후 Linear convolution과 같아지기 위해 어떻게 해야하는 지 알아보도록 하자.
1) 왜 Circular convolution이 되는가?
이 부분은 많은 학생들이 어렵게 받아들인다. 하지만 사실 이 글에서 살펴본 "DFT는 주파수샘플링이다!" 라는 말을 생각해보면 원래 샘플링이론이 시간영역에 적용되는 것으로 받아들일 수 있고 시간 상에서 신호가 주기화 된다는 것을 이해할 수 있을 것이다. 시간상에서 원래 finite 신호여야 하지만 주파수샘플링이 들어가는 DFT 후 다시 시간 상의 신호로 돌린다면 주기가 생겨 같은 신호가 앞뒤로 발생하기 때문에 원래의 convolution과 같을 수가 없는 것이다.

2) Circular convolution의 정의와 그 예제

X3[k](DFT coefficient)를 정의한다면, 시간축에서 아래와 같이 나타낼 수 있다.

물결표시의 경우 DFT한 신호를 다시 시간축으로 돌릴 때 생기는 주기적 확장을 뜻한다. x1[n]의 경우 어차피 0~N-1사이에 존재하기 때문에 modulo연산을 할 필요가 없어 위와 같이 변환이 가능하다. 마지막 식으로 Circular convolution을 정의한다. 위의 식을 간단하게 단계 별로 표현해보면 아래와 같다.
- x1[n]은 0~N-1까지로 그대로 둔다.
- x2[n]은 modulo shift를 하며 convolution연산(각 자리의 값을 곱하고 더하기)을 한다.
- 결과 x3[n]은 0~N-1까지만 값이 나온다.
예시를 보는 것이 이해가 빠르므로 아래의 예시를 참고하기 바란다.

3) Linear convolution과 Cirular convolution이 같아지려면?
결론부터 얘기하면 아래의 조건을 만족하면 된다. 즉, DFT point가 x1과 x2의 length를 더한 것에 1을 뺀 값보다 크거나 같으면 두 convolution의 값이 같아진다.

역시 예시를 살펴보자.

무한히 긴 신호의 Linear convolution의 계산: overlap-add, overlap-save
우리는 LTI system에서 output을 구하기 위해 Linear convolution을 계산하면 된다는 것을 안다.(convolution의 정의는 LTI임을 가정해야만 가능) 근데 FFT알고리즘의 개발으로 Linear convolution을 하는 것보다 DFT를 이용해 output을 구하고 inverse DFT를 하는 방식으로 linear convolution을 구할 수도 있게 되었다. 우리는 앞에서 DFT point N이 L+P-1보다 크거나 같으면 Linear convolution이 된다는 것을 알고 있다. 근데, 실제로 우리가 이용하는 신호들은 사실상 finite하기엔 너무 긴 신호들이 많다. 그래서 implementation을 하기 위해서는 짧은 finite 신호들로 쪼개서 block convolution을 해야한다. 이는 python에서 scipy library에서 signal.fftconvolve로 사용할 수 있고 긴 sequence에서 빠른 성능을 보인다.
1) Overlap-add
x[n]을 길이가 L인 finite한 block으로 쪼개고 Npoint까지 zero-padding한다. 쪼개진 신호들은 x0[n],x1[n]......이렇게 생성된다. 그리고 각각을 convolution한다.

2) Overlap-save
overlap-add에서 문제가 되는 것은 첫 부분은 앞에 overlap되는 부분이 없어서 부정확한 값이 나온다는 점이다. 쓰지 않는 앞부분을 더 추가하여 convolution을 계산하고 필요없는 앞부분을 다시 버린다.

Reference
Discrete-Time Signal Processing - Oppenheim
'Domain Knowledge > Speech' 카테고리의 다른 글
| LPC(Linear Prediction Coding, 선형예측부호화)와 formant estimation (0) | 2020.07.31 |
|---|---|
| Pitch detction(ACF, AMDF, Cepstrum) (0) | 2020.07.31 |
| Speech production and perception(음성의 생성과 인지) (0) | 2020.07.31 |
| 음성신호처리에서 frame 생성시 overlap을 하는 이유 (5) | 2020.07.30 |
| STFT(Short-Time Fourier Transform)와 Spectrogram의 python구현과 의미 (6) | 2020.07.30 |



