(26.12.11 몇가지 오류가 있어...글 전체 revise하였습니다.ㅎㅎ)
이제부터 두 개의 포스팅을 통해 머신러닝에 대한 확률적 접근에 대해서 살펴보도록 할 것이다. 기본적으로 이 접근법은 우리가 관심을 갖는 값 (모델, 클래스)이 고정된 상수가 아니라, 불확실성을 내포한 확률 분포에 의해 좌우된다는 생각에서 시작한다. 관측된 데이터와 함께 확률을 추론함으로써, 최적의 결정(Optimal Decision)을 내리는 것을 목표로 한다. 이번 글에서는 그 핵심이 되는 베이즈 정리(Bayes' Theorem)를 쉬운 말로 정리해보고, 이를 기반으로 파라미터를 추정하는 대표적인 두 가지 방법인 MLE (Maximum Likelihood Estimation)와 MAP (Maximum A posterior Probability) 에 대해 직관적으로 설명해보도록 하겠다. 엄밀히 말해 MLE는 빈도주의적 방법이고 MAP는 베이지안의 관점을 일부 차용한 점 추정(Point Estimation)이지만, 이 두 가지를 이해하는 것이 추후 다룰 베이지안 러닝(Bayesian Learning)으로 나아가는 첫걸음이 될 것이다. 또한 데이터 모델링에 사용되는 파라미터(weight 등)를 예측할 때, 이 방법들이 Least Square Solution과 같아지는 경우도 함께 알아보겠다.
Summary
- 베이즈 정리(Bayes' Theorem): 확률적 추론의 핵심 원리 이해
- MLE & MAP: 파라미터 추정의 양대 산맥인 MLE(빈도주의)와 MAP(베이지안적 점 추정)의 직관적 설명
- Least Square와의 관계: 확률 모델링이 어떻게 최소 제곱법과 연결되는지 증명
Bayes theorem

많이 본 식인데, 대학교때 확률과 랜덤프로세스를 배운 사람들이면 모두 아는 그 식이다. 이거 이용해서 시험문제 참 많이 나왔던 기억이....(코쓱)..... 바로 이 베이즈정리를 우리가 해석하려는 MLE/MAP에 관한 용어들과 함께 소개해보겠다.

- X: Observation, 관측된 데이터를 뜻한다. 우리가 갖고 있는건 이거다!! 머신러닝에서는 feature(입력변수)라고도 부른다. (관측값은 결국 표본임으로 실제 분포와 같지는 않다.)
- Θ: Hypothesis or Parameter, 관측된 데이터를 통해 추정하고자 하는 값이 되겠다. classification문제에서는 각 discrete한 클래스가 될 수 있고 linear regression의 경우 추정하려고 하는 weight들이 될 수 있다. 그 외에 추정하고자 하는 모든 문제에서 추정하고싶은 target값이 된다.
- P(X): Marginal probability, 데이터 X자체가 관측될 전체 확률, 모든 가능한 가설들에 대해 X가 나올 확률을 합한 값이다.
- P(Θ): A prior probability(사전확률), 사전에 Θ에 대해 가정하는 확률을 말한다. 이때 Θ는 mutually exclusive 해야한다. 예를들어, "동전의 앞면"/"동전의 뒷면" 이 두가지 가정은 동시에 성립될 수 없으며 두 확률의 합이 1이 되어야한다. (사전적으로 hypothesis에 대한 지식이 없을 때는 그냥 hypothesis의 element들이 가질 확률이 모두 같다고 두자, uniform distribution)
- P(X|Θ): Likeihood(우도), hypothesis를 두고 다시말해 어떤 가정을 한 상태의 데이터의 분포를 뜻한다.
- P(Θ|X): A posterior probability(사후확률), observation이 주어졌을 때의 hypothesis의 분포를 뜻한다. 얘같은 경우에는 데이터 X의 영향을 반영하는 애다. prior가 X를 만나 어떻게 변했는지를 나타내며, 베이즈정리를 통해 궁극적으로 우리가 구하고자하는 목표 값이다.
앞서 정의한 추상적인 용어들(Θ, X, Prior, Likelihood)이 실제 문제상황에서 어떻게 동작하는지, 그리고 왜 prior를 함께 고려하는 사고가 중요한지에 대해 아주 유명한 암진단 예시를 통해 구체적으로 살펴보자.
우리는 병원에서 검사를 받았고, 그 결과를 해석해야한다.
가설 Θ: 환자의 실제 상태 (알고싶은 것)
- cancer: 환자가 암에 걸렸다.
- not cancer: 환자가 암에 걸리지 않았다.
관측 X: 병원의 검사 결과
- +: 양성판정
- -: 음성판정
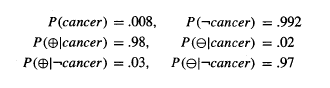
Likelihood만 본다면, 암인데 양성판정이 나올 확률이 0.98임으로 "검사결과가 양성판정이 나오면 암이라고 봐도 되겠네?" 라고 생각할 수 있다. 하지만 베이즈정리를 통해 냉정하게 확률을 계산해봐도 그럴까..?

양성인지 음성인지에 대한 확률은 normalize factor에 불과하므로 계산하지 않았다. (베이즈 정리 식에서 분모인 P(X), 즉 P(+)는 두 가설의 계산에 공통적으로 들어가므로 생략하고, 분자의 비례값만 비교한다.) Posterior를 계산한 결과, 양성판정을 받았음에도 불구하고 정상일 확률이 약 3.8배나 높은 것을 볼 수 있다. 따라서 베이지안 관점에서 "양성판정을 받아도 암이라고 볼수 없다." 라고 추론하는 것이 더 합리적이고 최적인 결정이 된다.
이처럼 베이지안 접근법은 눈앞에 보이는 데이터뿐만 아니라, 기저에 깔린 prior probability (해당 예시에서는 암 발병률이 매우 낮다는 사실)까지 종합적으로 고려하여 판단한다는 강력한 특징이 있다.
MLE vs MAP
앞선 암진단 예시를 통해, 우리가 최종적으로 어떤 결정을 내릴 때 데이터가 주는 정보 (likelihood)와 사전지식 (prior)을 어떻게 조합하느냐에 따라 결론이 완전히 달라질 수 있음을 확인했다. 이러한 접근방식을 좀 더 일반화하여 파라미터를 추정하는 2가지 방법론 MLE, MAP를 설명하려고 한다. 그에 앞서 두 방법론이 간략하게 뭐가 다른지를 설명하고 넘어가려고 한다.
일단 MLE와 MAP는 확률모델을 이용하여 어떤 변수(Θ), (e.g., 클래스 분류 Θ_1/Θ_2) 를 추정하는 방법이다. 두 방법 모두 full distribution을 구하지 않고 single estimate를 통해 파라미터 Θ를 추정한다.

여기서 P(Θ_1|X)(observation X가 주어졌을 때, 클래스 1일 확률)과 P(Θ_2|X)(observation X가 주어졌을 때, 클래스 2일 확률) 둘 중 더 큰 확률을 가지는 클래스를 고르면 observation에 대한 클래스를 고를 수 있을 것이다.

최종적으로 우리가 하고싶은 일은 posterior probability가 최대가 되게 하는 어떤 Θ값을 찾고싶은 것이다.
그래서 이걸 최대화 해야되는데?!

우리는 left-hand side의 값을 알 수 없다. 그렇기 때문에 베이즈정리를 이용해서 left-hand side와 등식이 성립하는 right-hand side term가 커지는 방향으로 Θ를 찾는 전략을 취한다. 그런데 분모에 있는 P(x)는 상수값으로 일정하므로 비례관계에서는 제외할 수 있겠다.
1) Maximum likelihood Probability (MLE)
P(Θ)를 제외시키고 Likelihood term만 최대로 만들고자 하는 방법을 Maximum likelihood Probability(MLE)라고 한다. 이렇게 하면 사전지식은 무시하고 눈앞의 데이터를 잘 설명하는 Θ를 고르게 된다.
2) Maximum A posterior Probability (MAP)
right-hand에 있는 전체 term(P(x)는 상수니까 제외하고)을 최대로 만들고자 하는 방법은 a posterior probability자체를 최대화하는 것으로 생각할 수 있겠고, 그것을 Maximum A posterior Probability(MAP)라고 한다. 아까 암진단 문제에서 봤던 prior를 고려하는 더 베이지안스러운 방법이다.
그래서 수식적으로 어떤 부분을 최대화하는 방법인지 두 가지를 비교해 보았다.
이제 자세한 수식은 아래 각각의 section에서 소개하도록 하겠다.
Maximum Likelihood Estimation(MLE)
Likelihood probability(우도) P(X|Θ)를 최대화 하는 어떤 변수(Θ)를 찾는 방법,

A posterior probability(사후확률)을 크게 하는 것은 Likelihood(우도)를 크게 하는 것이라고 생각하는 방식이다.
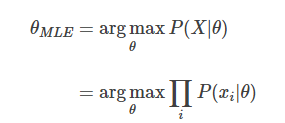
그래서 P(X|Θ)를 크게하는 Θ를 찾는 것이 MLE방법이 된다. (argmax는 최대값을 찾는 것이 아닌 최대값이 되게 하는 변수를 찾는 것이다.) 여기서 X벡터의 각각의 element에 대한 확률 곱으로 다시 P(X|Θ)를 만들 수 있다. (각 element가 mutually exclusive) 근데 여기서 P(xi|Θ)는 확률 값이므로 곱할 수록 0에 가까워진다.
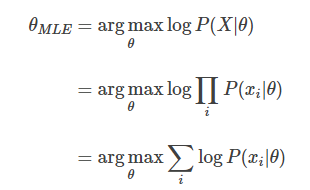
그래서 여기서 log를 취하게 된다. log는 단조증가함수이기 때문에, log를 취해도 똑같이 max값을 구하면 된다. log를 취하면 곱이 합으로 바뀌기 때문에 최종 MLE의 식을 완성할 수 있다.
Maximum A posterior Probability(MAP)
A posterior probability(사후확률) P(Θ|X)를 직접 최대화하는 어떤 변수(Θ)를 찾는 방법!
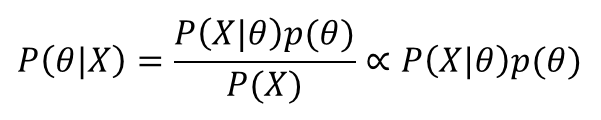
하지만 아까도 말했듯이 P(X)는 constant이다. Normalizing constant이기 때문에 비례식에서는 중요치 않으니까 제외시켜 위의 식의 가장 오른쪽 텀을 최대로 하는 클래스를 찾는다.
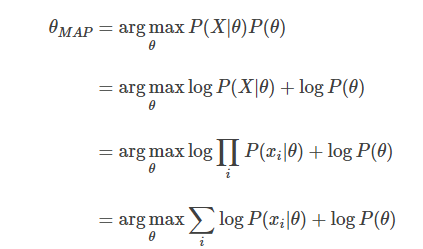
P(X|Θ)P(Θ)값을 최대로 하는 Θ를 찾으면 된다. MLE에서와 동일하게 log를 취하면 MAP식을 완성하게 된다.
MAP가 MLE와 같아지는 조건
MLE는 a prior probability가 uniform distribution이라고 가정한 MAP라고 볼 수 있다.
만약에 Θ가 uniform distribution이라면 어떤 일이 벌어질까?
uniform distribution을 따른다는 뜻은 분류문제를 예로 들었을 때, 클래스1과 클래스 2가 나타날 확률이 같다는 뜻이다. P(Θ1)=P(Θ2)=0.5로 상수값을 가질 것이다. argmax식에서 상수값은 최대화시키는 task에서 아무 영향을 미치지 못한다. 그래서 이는 식에서 빠지게 되고 결국 MAP가 MLE식과 같아지게 된다.

MLE/MAP와 Least Square solution
이번에는 특정 learning algorithm이 명시적으로 베이즈룰을 쓰거나 확률계산을 하지 않아도, MAP가정의 의미를 갖는다는 것을 보이도록 하겠다. 아까는 계속 hypothesis를 discrete한 클래스의 추정처럼 얘기했는데 이번엔 continuous한 값을 추정한다고 해보자. 이런 continuous한 값에 대한 문제들은 neural net이나 linear regression, 다항식커브의 fitting같은 다양한 학습알고리즘에서 사용된다.
근데!
"Training data가 gaussian noise에 의해 degrade되었다고 할 때, likelihood를 maximize하는 것은 squared error를 minimize하는 것과 같아진다."
왜 이런일이 발생하는 것일까?
우리가 어떤 데이터 분포를 모델링하고자 한다.

그렇다면 아래와 같이 가정하는 모델 f에 error를 더한 값으로 estimate될 것이다.
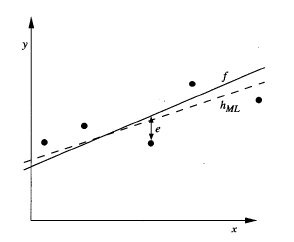
그리고 만약 모델 f가 선형이라면 위와 같은 그래프를 그릴 수 있고 h_ML라고 구한 점선은 noisy한 data를 가지고 ML solution을 구한 선이 되겠다. 확률을 구할때, continuous한 경우에는 pdf를 이용해야하지만 그냥 확률 값으로 쓸 수있다고 가정한다. h_ML은 아래와 같이 구할 수 있다.
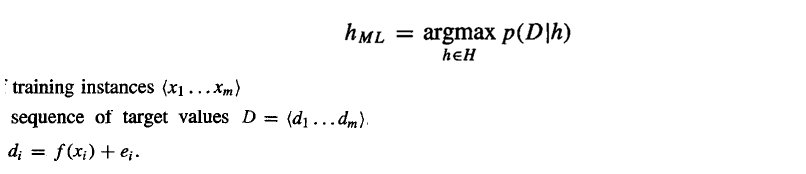
일때, 주어진 가정에 대해서 mutually independent하다고 하면 아래의 식으로 정리할 수 있다.

여기서 error ei가 정규분포(zero mean gaussian)를 따른다고 하자. 그러면 p(di|h)를 normal distribution에 관해 정리할 수 있다.

자 이제 log를 취해보자.

여기서 h와 관련없는 텀은 소거해도 상관없다. 이걸 최대화 하는 h를 구하고싶은거지 최대값을 직접 구해야되는거 아니니까!

여기서 '-'부호를 빼면 minimize문제로 둔갑할 수 있다.
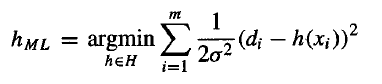
쓸데없는 상수텀을 빼보도록하자.

MLE와 Least square이랑 같아져버렸다....즉, '데이터의 노이즈가 가우시안 분포를 따른다'는 가정하에서는, Likelihood를 최대화(MLE)하는 것이 오차 제곱의 합을 최소화(Least Square)하는 것과 수학적으로 완전히 동일하다는 것을 증명했다. 해당 증명이 우리에게 시사하는 바는 매우 크다. 먼저 우리가 흔히 사용하는 MSE같은 loss function이 단순히 직관적으로 만들어진 것이 아니라 "노이즈가 정규분포를 따른다"라는 합리적인 확률적 가정에 기반하고 있음을 보여준다. 또 "확률 모델링"과 "오차최소화"라는 머신러닝의 두가지 큰 접근방식이 사실 맞닿아 있다는 것을 증명함으로써, 모델에 대한 통합적이 시각을 제공한다.
여기에 linear regression에 regulizer term을 추가한 ridge regression은 MAP와 같아진다는 결과도 있는데 아직 linear regression을 안했으니 다음에 언급해보도록 하겠다.
Reference
Machine Learning - Tom Mitchell
'ML&DL > Machine Learning' 카테고리의 다른 글
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |
|---|---|
| Naive bayes classifier(나이브 베이즈 분류기) 원리 (0) | 2020.06.13 |
| K Nearest Neighbor(K 최근접 이웃) 원리 (0) | 2020.06.13 |
| Decision tree(의사결정나무) 원리 (0) | 2020.06.13 |
| SVM(Support Vector Machine) 원리 (5) | 2020.06.12 |



