어떠한 '분류'라는 문제를 풀기 위해 패턴 인식 분야는 꾸준히 발전하였다. 가장 오랜 역사를 가진 통계적 분류방법에서 출발해서 신경망이 개발되었고 트리분류기, 은닉마코프모델등이 개발되었다. 이런 상황에서 SVM이 등장하여 주목받았다.
SVM은 기존의 분류방법들과 기본원리가 크게 다르다. 신경망을 포함하여 기존의 방법들은 분류 '오류율을 최소화'하려는 목적으로 설계되었다. 하지만 SVM은 한 발짝 더 나아가 두 부류 사이에 존재하는 '여백을 최대화'하려는 목적으로 설계되었다.
SVM이란 무엇인가?
기계학습 분야 중 하나로 패턴인식, 자료분석을 위한 지도학습 모델분류와 회귀분석을 위해 사용한다.
- 두 카테고리 중 어느 하나에 속한 데이터 집합이 주어졌을 때,
- 주어진 데이터집합을 바탕으로 새로운 데이터가 어느 카테고리에 속하는지 판단하는 비확률적 이진 선형분류모델을 만든다.
- 만들어진 분류모델은 데이터가 사상된 공간에서 경계로 표현되는데 SVM알고리즘은 그 중 가장 큰 폭을 가진 경계를 찾는다.
이러한 정의와 SVM의 패턴인식순서는 글로 읽었을 때는 도무지 이해가 안된다. 그러니 예를 통해 이해해보자. 간단한 SVM모델을 예를 들어 설명하자면, 짜장면인지 짬뽕인지 직선을 그어서 구분하는 것이다. 국물의 양과 고춧가루의 양이 많으면 짬뽕 아니면 짜장으로 구분할 수 있을 것이다.

어떤 이는 그 짜장면과 짬뽕사이의 여백이 가장 넓어지면(둘이 가장 떨어져 있으면(=margin최대화)) 그 둘을 가장 잘 분류했다고 생각할 것이다. 이러한 철학을 따라서 SVM은 "여백이 가장 넓어지는 저 빨간 선을 찾는 것"을 목표로 한다. 그림과 같이 빨간 직선(선형모델)으로 그 둘을 구분 할 수도 있고 문제가 복잡해짐에 따라서 때로는 직선이 아닌 구불구불한 곡선으로(비선형모델)으로 둘을 구분할 수 있을 것이다.
이렇게 직관적으로는 어려운 이야기가 아니지만 실제 이론으로 정리하여 구현하는 일은 쉽지 않다. 이제 전공스러운 벡터를 통해 이론으로 정리를 시작해볼 것이다. 조금 어렵지만 3번정도 읽으면 전공자가 이해할 수 있게 되도록 쉬운 방식으로 설명하고자 한다!! 가장 기초적인 유클리디안 평면에서 선형모델을 가지고 설명한다.
SVM의 decision rule
가중치 벡터 w와 직교하면서 margin이 최대가 되는 선형을 찾는다. 이 말이 받아들이기 어렵다면 위의 그림을 좀 더 수학적으로 표현한 아래의 그래프를 통해 이해해보자.

- support vector:두 가지 카테고리(짬뽕/짜장)에 각각 해당되는 data set들('-'샘플이 모인곳/'+'샘플이 모인곳)의 최외각에 있는 샘플들을 support vector라고 부른다. 이 가장 최 외각에 있는 벡터들을 토대로 margin M을 구할 수 있기 때문에 중요한 벡터들이다.
- margin: support vector를 통해 구한 두 카테고리 사이의 거리를 m이라고 하고 이를 최대화 해야한다.
우리가 가진 '+'샘플과 '-'샘플을 구분하기 위해 support vector를 통해 margin이 최대가 되는 빨간점선을 만들려고 한다. '+'샘플과 '-'샘플들은 선형으로 분리가 가능한 상황이다. 그러므로 직선을 통해 두 dataset을 분리하도록 하자. 이 때 이 직선을 결정 초평면(decision hyperline)부르기로 한다. 결정 초평면을 정의하기 위해서는 두 개의 매개변수가 필요하다. 결정 초평면에 수직하는 가중치벡터 w와 상수 b이다.
(+초평면이 무엇인가... 생소할 수도 있을 것 같아서 추가로 정리한다.
초평면은 어떤 N차원 공간에서 한 차원 낮은 N-1차원의 subspace를 말한다.
3차원의 경우 면이 되는 것이며, 2차원의 경우 선이 되는 것이다. 우리가 아래서 살펴볼 기본내용은 2차원을 다루므로
초평면이 선으로 결정되겠다. 아래의 내용은 법선벡터와 임의의 실수를 이용해 결정초평면을 결정하는 데 있어서
바탕이 되는 내용이다.)


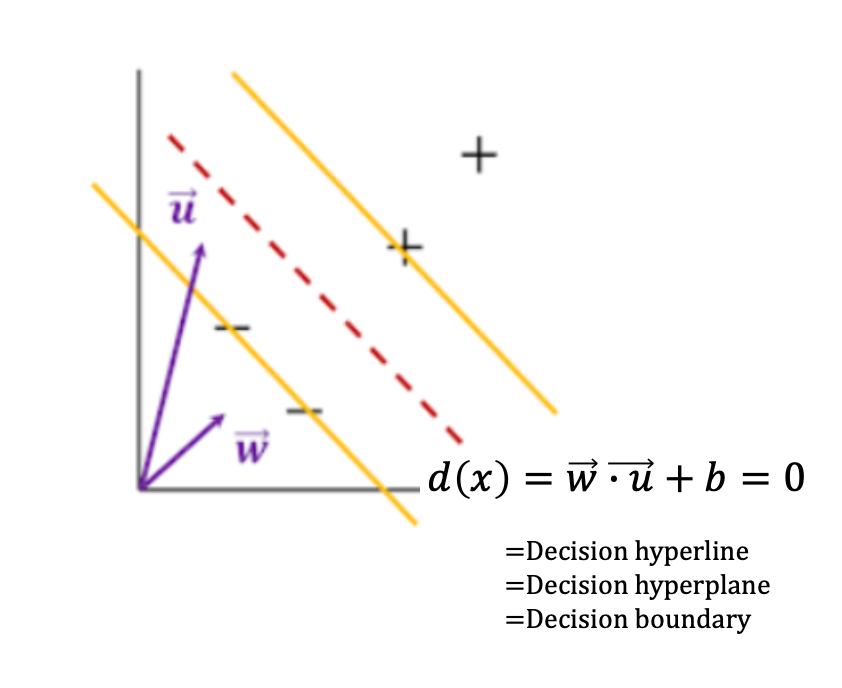
법선벡터 w와 결정초평면 위에 있는 벡터 x에 대하여, 결정 초평면의 식을 가정해 보자.
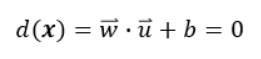
여기서, 가중치 벡터 w는 서포트벡터들 사이의 여백을 가장 크게 하는 초평면(여기선 line)의 방향을 뜻하게 된다. 그리고 b는 서포트 벡터들 사이의 여백을 가장 크게하는 결정 초평면의 위치를 뜻한다. 하지만 우리가 그릴 수 있는 직선은 여러가지 방법이 있을 것이고 그렇기 때문에 w와 b값은 아직 정할 수 없다. 우리는 앞으로 나올 여러가지 과정을 통해 w와 b값을 구해낼 것이고 이를 통해 초평면의 식을 완성할 수 있다!
여기서 우리가 궁금한 것은 이 새로운 샘플 u가 우리가 가정한 결정 초평면을 기준으로 , '+'샘플이 있는 쪽(왼쪽)에 속하느냐? 아니면 '-'샘플들이 있는 쪽(오른쪽)에 속하느냐?이다.

가장 간단하게 구분할 수 있는 방식은 내적의 값이 어떤 상수를 기준으로 그보다 큰지 작은지를 판별하는 것이다. 여기서 더 나아가 decision hyperplane(초평면)에 평행하고 초평면에서 가장 가까운 샘플인 support vector를 이용하여 위의 그래프의 노란선 두개를 정의해보자. 여기서 우리는 초평면과 '+','-'샘플들 사이의 거리를 같게 설정했으므로 임의의 decision hyperplane으로부터 동일하게 δ만큼 떨어져야 한다.

그런데, 어차피 w벡터도 모르는 수이고 b도 모르는 수이기 때문에 임의의 δ로 나누어 주어도 임의의 숫자이다. 그러므로 δ에 대해 정규화하여서 다음의 수식을 얻을 수 있다.

이러한 제약조건을 하나로 표현하기 위해 yi(클래스를 나타냄)라는 변수를 도입해보자..

이를 통해 두 식을 아래와 같이 하나로 정리할 수 있다.
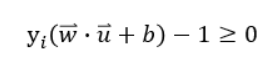
여기서 새로운 제약조건을 하나 만들겠다. 그것은 등호가 성립하는 경우는 각각 노란선에 샘플이 걸쳐있는 경우라는 것이다. 그러므로 등호가 성립할 때 support vector위의 그래프에 있는 노란선 두 개가 정의할 수 있다.

물밑작업을 끝났고! 다시 본론으로 들어와 이렇게 각각의 직선을 정의 했을 때, margin을 최대화 하는게 목적이다. 아래의 그래프를 통해 margin을 구해보자.

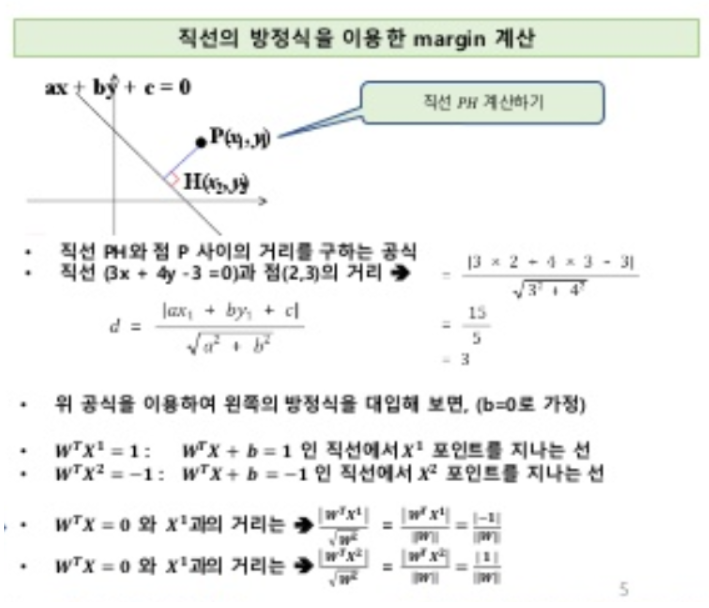

위의 식을 통해 margin의 width를 구할 수 있다.
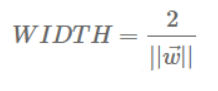
이를 최대화하는 것이 이제 과제가 되었다! 이것을 최대화하는 w와 b만 찾으면 된다.
Margin의 optimization
margin을 최대화 하는 문제는 조건부 최적화문제로 해석될 수 있다.

이는 라그랑주 승수법을 이용하여 풀 수 있다. 이 때 미분계산의 편리성을 위해 우리는 아래와 같은 행위를 할 수있다!
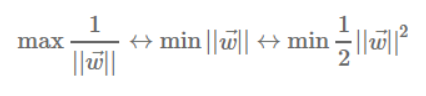

단숨에 문제가 이렇게 바뀐다. 이를 라그랑주 승수법을 이용하여 풀어보도록 하자.

라그랑주 함수로 표현한 조건부 최적화문제의 경우 보통 KKT조건을 이용하여 풀이한다. (어려우신 분은 구글에 라그랑주승수법을 검색해보시면 풀이법에 대한 자세한 설명을 확인하실 수 있습니다.)
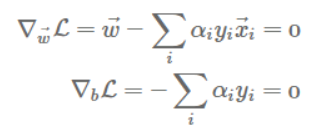
우리가 관심이 있는 변수들로 각각을 미분해주면 위의 두가지 식을 도출해낼 수 있다. 이 두개의 식 중 첫번째 식을 통해 우리는 가중치벡터 w를 얻을 수 있다.
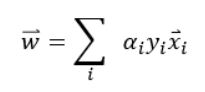
여기서 알 수 있는 사실은 w벡터가 샘플 x들의 선형조합으로 이루어져 있다는 것이다. 여기서 우리는 a값만 알게 되면 벡터w값을 알아낼 수 있다는 사실도 깨닫는다. 위의 두 식을 통해서 라그랑주 함수를 정리해 보자.
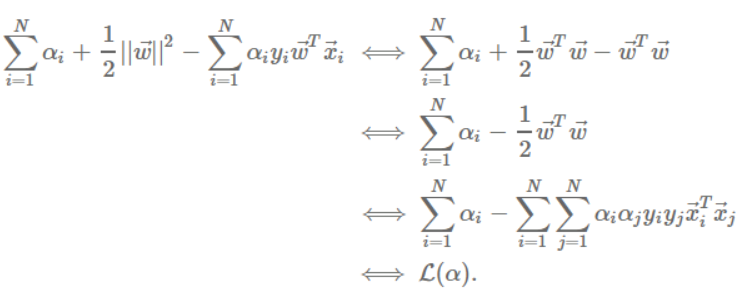

이제 식은 이렇게 정리된다. 이 식을 통해 a값을 구할 수 있고 이어서 w값도 구할 수 있으며 제약조건을 통해 b값도 구할 수 있게 된다. 이를 통해 모든 변수를 구하고 우리는 결정초평면을 구할 수 있다. 제약조건에 의해 a값이 0이 아니라는 것은 해당 샘플이 경계선에 있는 샘플이라는 뜻이고 이 샘플을 support vector라고 부른다.
※제약조건:yi( w·xi+b)−1≥0(등호가 성립할 때 support vector)
Soft-margin SVM
지금까지 훈련 데이터 포인트들이 특정공간상에서 선형적으로 분리가 가능하다고 가정했다. 하지만 실제 사례에서는 클래스 조건부 분포간에 중첩이 존재할 수 있다. 이런 경우에 훈련데이터들을 정확하게 분리하려고 모델을 훈련시키면 일반화가 안될 수 있다.(overfitting문제)
그렇기 때문에 몇몇 training data에 대해 잘못 분류되는 것을 허용하는 방식으로 SVM을 수정할 수 있다. 원래의 SVM은 잘 못 분류되었을 때, 무한대의 오류를 주고, 잘 분류되었을 때, 0의 오류를 준다. 이제 이 방식을 수정해서 데이터 포인트들이 잘못된 쪽애 존재하는 것을 허용하도록 해보자. 근데 경계로 부터 멀어질 수록 불이익을 주기로 하겠다.
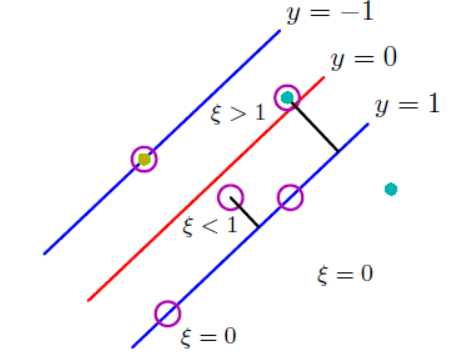
이 불이익을 거리에 대한 선형함수로 만들면 추후의 최적화문제를 풀기에 용이하기 때문에, 새로운 변수를 도입할 것이다. 그 변수는 느슨하다는 뜻에 slack variable ξn을 도입할 것이다. 아 변수는 직선을 그었을 때, 내가 속한 클래스와 내 원래 y값의 차이를 뜻한다.

y=+1인 클래스의 데이터 포인트인데 직선을 그었을 때,
ξn>1이라면, 잘못 detect된 data를 말한다.
ξn=0 이라면, 그 data point가 각 클래스의 support vector라는 뜻이다.
0<ξn≤1이라면, y=-1과 y=1사이 margin안에 있는 data라는 뜻이다.
그러므로 이 slack variable은 내 클래스가 아닌쪽으로 거리가 더 멀어질 수록 값이 커지게 된다.
slack variable을 도입해서 decision rule을 조금 수정할 수 있다.
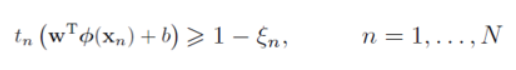
원래 식에 slack variable을 추가한 식이다. ξn는 0보다 크거나 같아야 한다. (잘못 분류된 녀석) 이렇게 slack variable을 빼주면 그만큼 여유를 주는 셈이 된다. 그러나 이렇게 했을 때, 오분류에 대한 불이익이 선형적으로 증가하게 된다. 그래서 우리의 다음 목표는 마진경계에 잘못된 쪽에 존재하는 포인트들에 약하게 불이익을 주면서 마진을 최대화하는 것이다.

오분류된 녀석들은 모두 ξn가 1보다 큰 값을 가지기 때문에 이를 다 더하면, 오분류된 포인트의 숫자의 upper bound가 될 것이다. 따라서 C는 정규화계수에 해당한다.(training error와 모델복잡도 사이의 trade off조절) C가 작다는 말은, constraint가 무시된다는 뜻으로 큰 margin을 갖게 된다. C가 커질수록 margin은 작아지고, C가 무한대가 되면 original SVM과 같아진다.
Reference
패턴인식, 오일석
http://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html#mjx-eqn-eqdr
https://www.slideshare.net/freepsw/svm-77055058
http://jaejunyoo.blogspot.com/2018/01/support-vector-machine-1.html#mjx-eqn-eqdr
'ML&DL > Machine Learning' 카테고리의 다른 글
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |
|---|---|
| Naive bayes classifier(나이브 베이즈 분류기) 원리 (0) | 2020.06.13 |
| Bayes theorem(베이즈정리)와 MLE/MAP (8) | 2020.06.13 |
| K Nearest Neighbor(K 최근접 이웃) 원리 (0) | 2020.06.13 |
| Decision tree(의사결정나무) 원리 (0) | 2020.06.13 |



