이 블로그는 단순히 내가 공부하는 내용을 정리하고자 글을 올리는 공간이다. regression을 이해하는데 참고한 사이트들을 통해 내가 이해한 방식대로 써내려갔다. 이곳 과 이곳 그리고 이곳을 이용해 포스팅을 했다는 것을 말하고 시작하겠다.
머신러닝을 한번이라도 공부해본 사람이라면 regression(회귀)에 대해 들어봤을 것이다. linear regression과 logistic regression 두가지 방법이 있는데, 둘의 차이를 간단히 정리해보면, linear regression은 target값으로 실수값을 예측할 때 사용하는 방법이고 logistic regression은 classification을 할 수 있는 regression으로 정수값을 예측할 때 사용하는 방법이다. binary classification을 하고 싶다면, target값으로 binary(0이나1)값을 갖게 되고, multiclass classification을 하고 싶다면, target값으로 정수값을 갖게 된다. 더 자세한 내용은 아래에서 설명하도록 하겠다.
Regression(회귀) 이란?
나는 공부하면서 회귀라는 말의 의미가 참 이해가 안되었다. 그냥 regression이란 "실수값을 예측하는 것, 근사치를 구하는 것"정도로 생각하고 넘어갔는데, 이 포스팅을 통해 한번 정리해보고자 한다. regression은 한국어로 바꾸면 회귀라는 말이다. 무엇을 회귀한다는 것일까...? 차근차근 알아보도록 하자.
회귀모델이라는 것은 어떤 연속형 변수 y를 y의 원인이라고 추정되는 x와의 관계를 통해 추정하는 것이다.
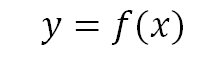
여기서 y가 target이 되겠고 이는 실수값을 갖는 연속형 데이터가 된다. 그리고 원인이 되는 x를 어떤 f()라는 회귀 모델을 이용해서 추정하는 것이다. 하지만 이런 추정을 통해 두 식이 같다고 할 수 없다. 왜냐면 추정이 완벽히 원래 target과 같을 수 없기 때문이기도 하고, 데이터 자체에 잡음(noise)가 있기도 하기 때문이다. 여러가지 요인에 의해 error가 생기게 되고 이를 고려해 위의 등식을 수정하면 아래와 같다.
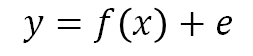
이제 회귀란 단어로 다시 돌아가보자. 회귀라는 용어는 '한바퀴를 돌아 다시 제자리로 돌아오다.'라는 뜻이다. 무엇이 어디로 회귀하는 것일까..? 아까의 식을 조금 변경하면 error에 대해 정리할 수 있다. 이런 error를 residual(잔차)이라고 부르겠다.

출처의 포스팅에서 말하는 회귀라는 것은 이 residual(무엇에 해당)이 기댓값 0(어디로에 해당)으로 회귀하는 것을 말한다. 우리는 그저 regression modeling을 하고 오차의 합을 최소로 하는 선을 찾는 모델을 회귀모델이라고 생각하지만, 사실은 이 말은 반만 맞다. 왜냐하면 사실 이 모델의 전제조건이 있다. residual이 iid를 만족해야 하기 때문이다. 위의 조건을 만족하지 않으면 오차의 합이 최소라고 해도 회귀모델이 되지 않는다.

우리는 모델링을 할 때, 일단 관계식을 추정해야하고 관계식을 추정한 후에 파라미터를 추정해야 한다.
둘 중 하나라도 잘 못 추정하면 정확한 회귀모델을 만들 수 없다. 만약 관계식을 선형모델링 했는데 사실 선형으로 표현할 수 없다면(모델 관계식을 잘 못 추정), 아무리 weight라는 파라미터를 잘 추정해도 정확한 회귀모델이 아니다. 그러므로 이에 따른 오차가 생기게 된다. 그리고 만약 관계식을 잘 추정했다고 했다면 ,이를 이용해 weight 파라미터를 추정하면 올바른 회귀식을 만들 수 있다.
하지만 모델의 관계식을 잘 추정했다고 하더라도, 모델과 실제 target에는 오차가 발생하게 된다.(데이터의 noise라던가..) 결국 어떤 상황이든 실제값과 추정값 사이에는 차이가 생긴다. 하지만 차이는 모델의 관계식을 잘 추정했다면 모델과 실제 target사이의 residual이 평균이 0으로 수렴하지만, 그 반대의 경우에는 아니라는 것이다. 만약에 우리가 관계식을 잘 모델링했다고 하면 residual(잔차)가 정규분포를 따르게 될 것이다.(정규분포가 원래 error의 분포)

좀 더 엄밀한 regression의 의미에 대해서 알아봤다. 간단히 정리해보자면, 실수형!!변수를 예측하는데, 그 추정값과 target의 차이(residual)가 평균0으로 회귀하는 모델!이라고 보면 되겠다.
Linear regression
이제 이 와중에 가장 간단한! linear regression을 알아보겠다. linear라는 말에도 나타나듯이 선형으로 모델의 관계식을 모델링하겠다는 뜻이다. 무엇이 어떻게 선형이라는 것인지 알아보도록 하자. 제일제일 간단한 모델을 살펴보겠다. 아래와 같이 우리는 x라는 1-dimension의 데이터에 가중치w를 곱하고 bias를 표현하기 위해 w0을 추가했다.

그럼 아래의 그림과 같은 빨간점의 데이터를 직선으로 표현할 수 있게 된다.
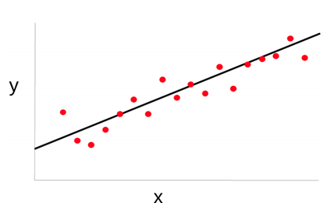
근데 사실은 데이터가 이렇게 직선형태로만 존재하지는 않을 것이다. 그렇기 때문에 이를 모델링하기 위해서 x와 y의 관계식에서 x를 어떤 h라는 함수에 통과시켜 사용할 것이다. 이게 무슨말일까... 일단 식으로 써보면,

여기서 h라는 함수는 이제 basis function이라고 부를 것이다. x의 기저를 바꾸는 행위를 통해서 데이터를 여러 모양으로 표현가능하다. 만약에 우리가 polynomial(다항식) basis를 사용한다고 하자. 그러면 아래의 그림과 같이 포물선 형태의 모델을 얻을 수 있을 것이다.
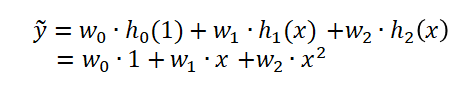
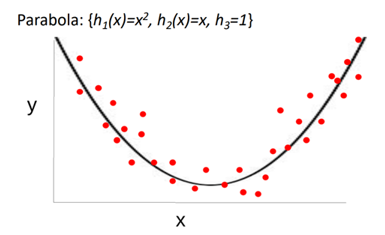
그럼 포물선 형태로 모델링을 했는데 왜 linear regression이냐... 할 수 있지만, 기저함수와 weight의 선형조합으로 target값을 예측했다는 것을 알 수 있다. 그래서 이런 모델링을 linear regression이라고 한다. 좀 더 general하게 추정한 값을 식으로 정리하면 아래와 같다.
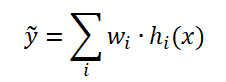
이를 원래의 target 값인 t(x)와의 차이의 제곱을 최소화 하는 weight를 찾으면 모델을 완성할 수 있다. 이렇게 single input으로 x값이 하나만 들어올 수도 있지만, 사실 input으로 들어오는 데이터는 여러 feature들을 갖는 벡터형태로 들어오게 된다. 벡터형태로 들어오게 될 경우로 general하게 weight를 구해보면 제곱의 합을 최소화 하는 방식으로 weight vector를 찾을 수 있다.
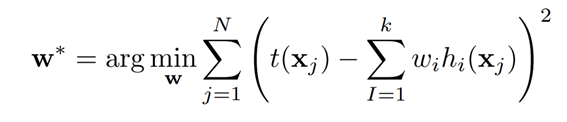
matrix notation으로 weight vector를 구하는 식을 풀어볼 수도 있다.
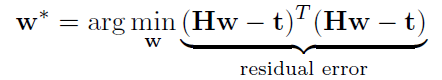
이 식은 미분이 가능하기 때문에 closed form solution을 얻을 수 있다.
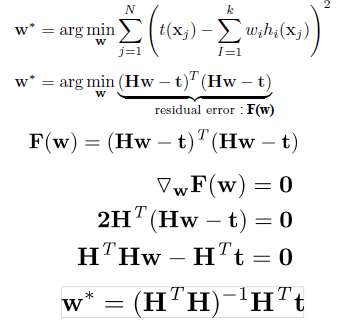
이렇게 최적화방법을 따로 둘 필요없이 해를 구할 수 있었다. 여기서 기저함수 h()는 polynomial이 아닌 가우시안 함수나 sigmoid함수가 될 수도 있다. 비숍의 패턴인식과 머신러닝책에서 여러 basis function의 그래프를 가져왔으니 참고하면 좋을 것 같다.
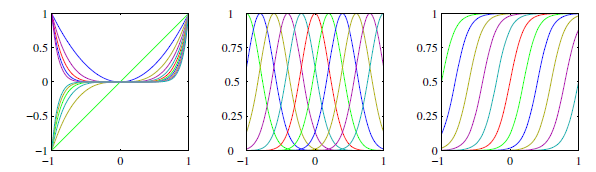
각각 polynomial, gaussian, sigmoid순이다.
Logistic regression
classification을 해결하는 다양한 방식이 존재한다. 가장 간단한 방법으로는 판별함수를 만들어 활용하는 방식(discriminative)이다. 또 하나의 강력한 방법은 추론단계에서 조건부확률(데이터가 주어졌을때 클래스의 확률)을 모델링하고 이 분포를 이용해서 최적의 결정을 내리는 방식이다. 이는 조건부확률을 parameteric 모델로 표현하여 최적의 파라미터를 훈련 데이터를 이용해 찾아낼 수 있다. 조건부확률의 모델링을 generative모델로 할 경우, 직접 클래스조건밀도와 서전확률을 모델링 한 후 사후확률을 그냥 베이즈정리를 이용해 구한다.
그 중에서도 우리는 가장 유명한 discriminative model중 하나인 logistic regression을 알아볼 것이다. 왜 근데 분류모델이 regression인가 싶을 것이다. regression은 실수값을 매핑하는 모델로 앞서 살펴봤기 때문이다. 결론부터 이야기해보자면, 확률을 regression한다는 의미를 담고 있다. 이는 뒤에서 더 자세히 보도록 하겠다.
다시 logistic regression이 뭔지에 대한 물음으로 돌아오자. logistic regression이 왜 생겨났는지에 대해서 부터 살펴보면서 그 물음의 답을 찾을 수 있다. linear regression은 weight와 기저함수의 선형조합으로 모델링을 한 후, 적절한 weight를 찾아 실수y값을 매핑했다.
쉬운 예제로 나이(x)를 통해 혈압(y)를 예측하려고 한다면, 직선을 쭉 그어서 데이터를 잘 표현 할 수 있다.
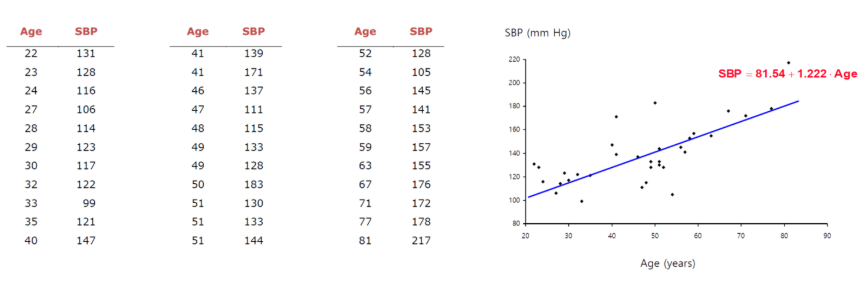
근데 이런 실수값을 찾는 것이 아닌, 암 발생여부와 같이 discrete(이산적인)값(발생:1, 안발생:0)을 찾아야 된다고 하자. 그럼 선을 쭉 그어서 y값을 추정하기는 어려워진다. 오른쪽 데이터 분포를 보면, 선형이라고 절대 보기가 어렵다.

y값이 극단적으로 0,1만 가지고 중간에 값이 없기 때문에 생긴 일이다. 아까의 혈압과 다르게 숫자 자체로 의미를 가지는 것이 아니다. 그러므로 0과 1을 바꿔도 사실 상관이 없다. 그럼 이런 이산적인 값은 어떻게 추정해야할까? 이걸 해결하기 위해 logistic regression이 나오게 된다. logistic regression을 정의하기 위해 필요한 두가지 개념,
1.logistic function
2.odd
을 먼저 소개하고 시작하겠다.
1.logistic function
아까 본 암발병여부 데이터를 모델링 하기 위해 logistic function이 나오게 되는데 아래와 같은 그림이다.
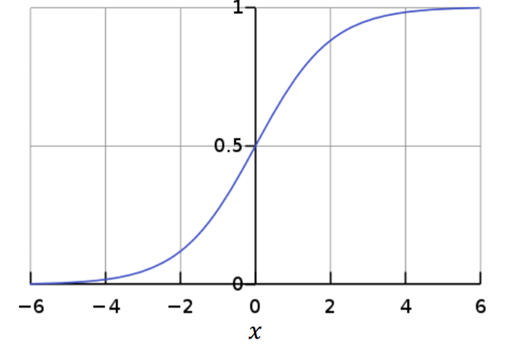
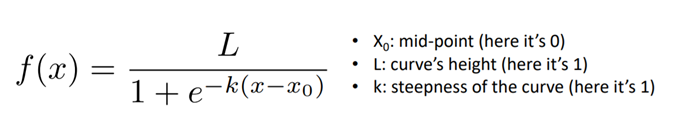
여기서 X0,L,k를 위의 설명과 같이 setting하면 이를 sigmoid함수라고 한다.

이 함수는 x값으로는 어떤 값이든 갖을 수 있지만 y값은 0~1사이만 나오게 된다. 0~1사이라고 하면 하나 떠오르는 게 있다... 그것은 확률!!! 이 함수는 확률밀도함수의 요건을 충족시킨다. 그리고 연속적이고 smooth한 것이 미분하기도 딱 좋다. 그리고 mirror symmetric한 것이 여러 application에 적용하기 좋게 생겼다. 그리고 미분도 간편한데, 미분연산 필요없이, 아래의 식으로 대체할 수 있다.

여튼 이런 logistic function을 이용할 것이란걸 염두해 두자.
2.odd(승산)
그리고 또 하나 알고넘어가야 할 것은 odd라는 개념이다. 이 것은 사건이 발생하지 않을 확률과 발생할 확률사이의 비를 나타낸다.
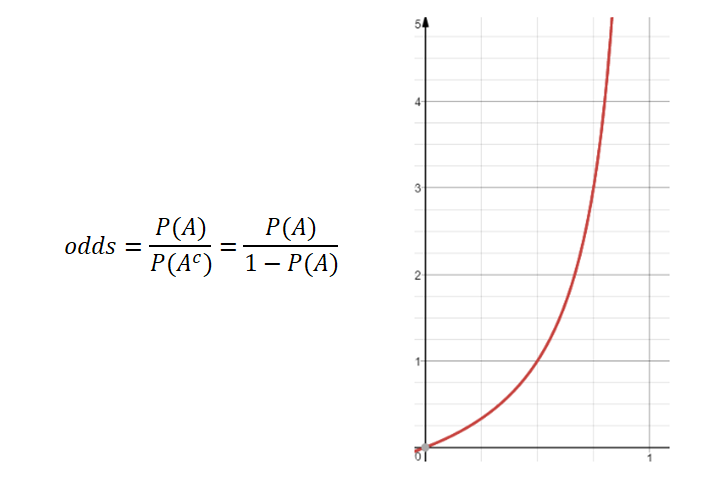
A가 발생할 확률이 커질수록 발생하지 않을 확률은 0에 가까워지고 전체 odd는 무한대로 치솟을 것이고,
A가 발생할 확률이 0이 되면 odd값은 0의 값을 가질 것이다. 그래서 그래프가 위와 같이 나타난다.
이제 logistic function과 odd를 이용해서 logistic regression을 정의해보자. 다중선형회귀의 식을 먼저 살펴보자. 설명변수x가 p개 존재할때, 식을 정의해보면 아래와 같다.

이때 weight를 β로 표현했고 회귀식은 살리되, y를 실수값이 아닌 확률 값을 가지도록 설계해보자. 좌변만 데이터 X가 주어졌을 때의 클래스 확률로 바꿨다.
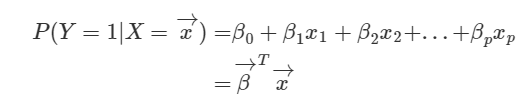
하지만 좌변은 0~1값을 가지는 것에 비해 우변은 [-∞,∞]값을 가진다. 그러므로 식을 수정할 필요가 있다. 아까 살펴봤던 odd식을 좌변에 넣어보자.

이렇게 해도 앞서 살펴봤듯이 odd는 [0, ∞]값을 가지기 때문에 mapping이 되지 않는다. 여기서 좌변에 log를 취하면 [-∞,∞]의 값을 갖게 된다.
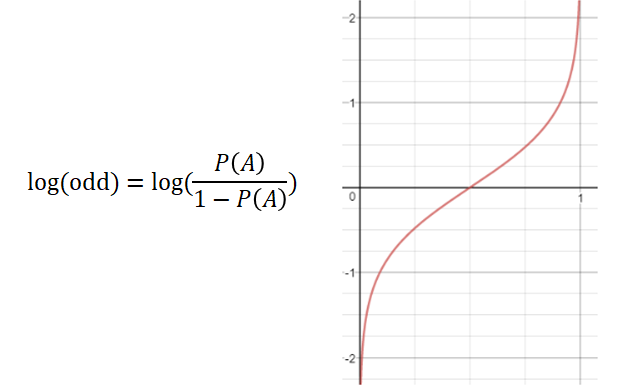
이를 종합해서 최종 식을 다시 써보면 아래와 같다.

여기에 exponential을 양변에 취해서 조건부확률에 대해 정리하게 되면,
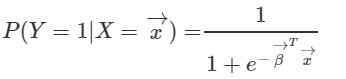
오호... 이것은 앞에서 많이 보았던 식이다. 아까 봤던 logistic function이 나왔다. 그래서 regression으로 추정한 식이 logistic function을 통과한 결과라고 볼 수도 있겠다. 그리고 나머지 Y=0에 대해서도 구해보면, 아래와 같다.

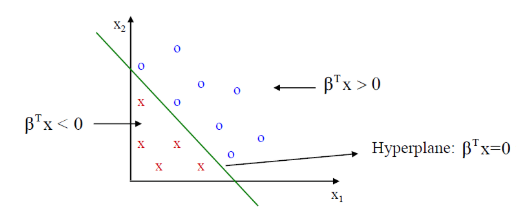
이렇게 조건부확률을 logistic function을 이용해 구해봤다. 이를 이용해 이제 classification을 할 수 있다. 그걸 어떻게 하는지 이제 알아보도록 하자. classification에서는 decision boundary(decision surface)라는 경계를 바탕으로 구역을 나누게 된다. 지금 살펴본 것은 Y=0,1로 두개의 class가 있기때문에 두 영역을 구분하는 decision rule을 만들어보자. Y=1로 분류하고 싶다면, 가장 간단하게 할 수 있는 방식은 아래와 같다.

좌변을 p(x)로 치환해서 이를 정리해보면,

이를 통해 weighted sum이 0보다 큰 것을 Y=1로, 그 반대는 Y=0으로 정할 수 있다.
Reference
크리스토퍼 비숍--패턴인식과 머신러닝
https://brunch.co.kr/@gimmesilver/17
https://ratsgo.github.io/machine%20learning/2017/04/02/logistic/
'ML&DL > Machine Learning' 카테고리의 다른 글
| Kernel/Kernel trick(커널과 커널트릭) (4) | 2020.06.13 |
|---|---|
| Regularization(정규화): Ridge regression/LASSO (0) | 2020.06.13 |
| Naive bayes classifier(나이브 베이즈 분류기) 원리 (0) | 2020.06.13 |
| Bayes theorem(베이즈정리)와 MLE/MAP (8) | 2020.06.13 |
| K Nearest Neighbor(K 최근접 이웃) 원리 (0) | 2020.06.13 |



