이 강의를 보고 정리한 내용이고 자료도 강의에서 가져온 자료임을 밝히고 시작한다. 이전 포스팅에서 살펴본 linear regression 모델을 다시 살펴보자.
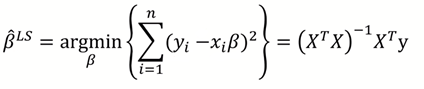
이렇게 least square solution을 구하면 너무 모델이 복잡해진다는 특징이 있다. (weight가 너무 커져서 모델이 너무 요동치게 된다...)
사실 데이터의 갯수가 많아지면 overfitting의 문제가 해결되는데 도움이 된다. 하지만 우리가 가지는 데이터의 수는 한정되어있을 가능성이 높다. 비교적 복잡하고 유연한 모델을 제한적인 숫자의 데이터 집합을 활용하여 fitting하려면 어떻게 해야할까? 과적합문제를 해결하기 위해 자주 사용되는 기법 중 하나는 바로 regularization(정규화)이다.(이를 penalization이라고도 한다.)
Bias와 variance의 trade-off
정규화 개념을 살펴보기 전에 앞서 살펴본 에러의 제곱의 기댓갑은 아래와 같다.
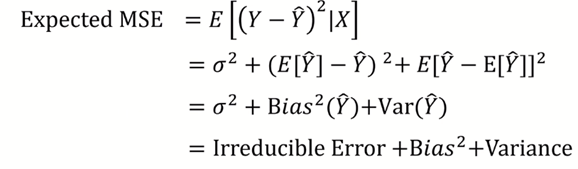
얘를 줄이고 싶다. Irreducible error는 모델로서는 어떻게 할 수 없는 에러이다. 그래서 bias와 variance term을 줄임으로서 에러를 줄일 수 있다. bias와 variance에 대한 직관적인 이해를 해보자면,

이 그림에서 보는 것과 같이 bias가 작다는 것은 과녁에 잘 편향되어져있다는 뜻이다. 그리고 variance가 작다는 것은 얼마나 흩어져있냐를 말한다. 그래서 둘을 다 줄이는 것이 좋은데, 사실 둘은 trade-off 관계가 있다.
앞서 살펴본 least sqare solution은 사실 가중치를 나타내는 weight에 대해, unbiased estimator중에서 분산이 제일 작은 걸로 고르는 과정이다. but,,,,unbias를 약간 희생하더라도 분산을 좀 더 줄이면 더 좋지 않을까? 라는 생각을 할 수 있다. bias가 좀 증가하더라도 variance를 감소시키자! 이걸 regularization(정규화)로 구현할 수 있다.
간단한 상황을 이용해 알아보도록 하자. h()가 polynomial이고, 1D input x가 있다고 하자.

이렇게 데이터가 뿌려져있다고 했을 때, 이를 1차함수로 예측하느냐 4차함수로 예측하느냐 여러가지로 할 수있게 되는데, 4차함수처럼 너무 복잡한 모델로 설정했을 때는 너무 variance가 커져서 test data에 대해 잘못 예측할 가능성이 높아진다. 그렇기 때문에 모델에 어떤 제약을 가함으로서 모델을 단순화할 수 있다.
하지만 너무 또 제약을 많이 가하면 bias가 커지고 모델이 너무 단순해져서 data에 대해 잘 표현하지 못할 수 있다.
Regularization
그래서 둘 사이를 잘 조절하는 것이 중요하고, least square solution으로 training data에 overfit한 모델을 만들었을 때, 혼란스러운 것을 뭔가 제약을 주어서 정돈한다라는 의미로 regularization(정규화)를 받아들이면 좋을 것이다. 그럼 정규화를 어떻게 할 것인가에 대해 알아보자.

4차 모델을 만들었을 때, 각각의 베타값이 존재하게 된다. 이럴때 높은 차수의 베타값을 없애준다면 모델을 단순화 할 수 있다. 그럼 베타값을 어떻게 없앨까...? 대표적인 방식으로 ridge regression과 LASSO가 있다. 각각 하나씩 살펴보자.
Ridge regression
처음 살펴볼 것은 L2 normalization을 이용한 제약을 가하는 것이다.

베타의 L2 norm을 어떤 범위로 제약을 주는 것이다. 그렇게 되면, 이 범위안에서의 최적의 베타를 구해야된다. 이를 라그랑주승수법으로 표현하면 아래와 같다.

이렇게 ridge regression식을 완성했다. 예시를 하나 들어보면,



이렇게 베타3과4에 5000이라는 람다값을 줬다. 그렇게 되면 최소화를 시킬때 베타3과4는 거의 0값을 가져야 최소의 error를 가질 수 있을 것이다. 그래서 이렇게 베타의 영향력을 감소시켜서 모델을 단순화할 수 있는 것이다. L2 regularization와 squared error의 관계를 그래프로 알아보기 위해 MSE의 형태를 알아보자.

2차식을 풀어서 전개하자.
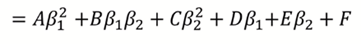
풀어서 전개한 식의 판별식으로 그래프의 모양을 알 수 있는데, 코시-슈바르츠 전개에 의해서 판별식이 0보다 작고, 그래서 타원형의 모양임을 알 수 있다.

이제 베타가 1,2가 존재할 때, 에러를 살펴보면, least square error에서 좀 더 키워서 ridge제약과 만나게 한다. (ridge의 제약이 제곱의 합이기때문에 원으로 표현된다.)

그래서 이 원과 딱 맞닿는 부분을 살펴보녀 거의 베타2가 0으로 가는걸 알 수 있다. 그래서 모델이 좀 더 단순화 되는 것을 살펴볼 수 있다. 제약이 무한대로 가면 베타1과2가 0이 되겠지만 이런 상황에서는 거의 0은 되지만 0이 아닌 값을가지는 것을 확인할 수 있다.
ridge regression은 미분이 가능하기 때문에 closed form solution을 갖는다.

LASSO(Least Absolute Shrinkage and Selection Operator)
다음으로 살펴볼 것은 L1 normalization을 이용한 제약을 가하는 것이다.

아까와 같이 라그랑주 승수법을 이용해 아래와 같이 나타낼 수 있다.

아까와 같은 방법으로 least square solution과 LASSO제약조건이 만나는 부분을 찾아보자.

LASSO는 제약이 절대값이기 때문에 마름모로 나오고 뾰쪽 튀어나온 부분이 베타가 0이 될 수 있다. 그래서 이그림에서 보면 베타2가 0이 되고 아예 그 변수가 사라지는 feature selection효과를 얻을 수 있다. 하지만 LASSO는 저렇게 뾰족한 형태를 가지고 있어서 미분이 불가능하다. 그래서 closed form solution을 얻을 수없고 convex formulation을 띄고 있어 numerical optimization기법을 활용해서 최적화를 해야한다.
정리하자면, 람다를 조절함에 따라 overfitting을 방지할 수 있다.

'ML&DL > Machine Learning' 카테고리의 다른 글
| K-means clustering(K-평균 군집화) 원리 (0) | 2020.06.13 |
|---|---|
| Kernel/Kernel trick(커널과 커널트릭) (4) | 2020.06.13 |
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |
| Naive bayes classifier(나이브 베이즈 분류기) 원리 (0) | 2020.06.13 |
| Bayes theorem(베이즈정리)와 MLE/MAP (8) | 2020.06.13 |



