앞선 포스팅에서 살펴본 실질적인 bayesian learning method중 하나가 naive bayes learner이다. 이를 niave bayes classifier라고 부르기도 한다. 이 방법은 몇몇 domain(예를들면, NLP)에서 neural net이나 decision tree와 비등한 성능을 냈다. 새로운 instance를 분류하는 bayesian approach는 instance를 표현하는 특징벡터가 주어졌을때, 가장 probable한 target(class)를 찾는 것이다.
Bayes theorem
다시 앞선 포스팅에서 봤던 베이즈정리를 정의해보자.

우리가 하려는 분류문제에 맞게 변수를 정의해보자면,
y는 분류하고자 하는 class가 된다.
X는 input의 특징벡터가 된다.
X를 각 element를 나타내는 형태로 표현하면 아래와 같다.

n-dimension의 특징벡터로 X를 위와 같이 표현할 수 있겠다.
Naive bayes classifier의 assumption: conditional independence
naive bayes classifier는 naive라는 뜻처럼 조금 순진한(?)방법이다. 주어진 class에 대해서 각각의 특징들이 어떤 상관관계가 있는지 따져봐야 하지만 naive bayes classifier같은 경우 모두 conditionally independent하다고 가정한다. 기본적인 bayesian 방법에 임의의 bias를 걸어준 것으로 볼 수 있다. 임의의 두 feature가 있다고 했을때, joint probability를 각각의 probability의 곱으로 표현가능하다.

더 general하게 n개의 feature에 대해 표현해보면,

이럴 경우 복잡한 joint probability에서 벗어나 문제를 단순화 할 수 있다.
Naive bayes classifier의 decision rule: MAP
naive bayes classifier는 기본적으로 bayesian learning이기 때문에 a posterior probability를 maximize하는 class로 말그대로 most probable한 결정을 내리려고 한다. 그래서 이를 수식으로 정리해보자.
다시 베이즈 정리를 정의해보면,

여기서 특징벡터X를 n개의 element에 대해 풀어서 써보면 아래와 같다.

여기서 아까 가정했던 conditional independence를 적용해보면, 아래와 같이 풀어쓸 수 있다.
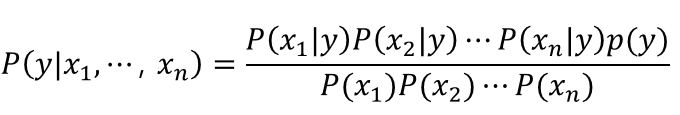
우리가 argmax하는 문제에서는 사실 각각의 값이 중요하지 않다. 특히 X에 대한 확률은 상수값을 가지므로 무시할 수 있다.
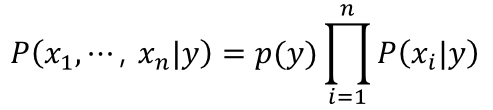
그럼 a posterior probability는 오른쪽 term에 비례하는 것을 알 수 있다. a posterior probability 를 최대화하는 것은 오른쪽 term을 최소화하는 문제와 같아지게 된다.

그래서 최종 추정class에 대한 식은 이식을 최대화 하는 것이되고 이것이 naive bayes classifier의 decision rule이다.
Naive bayes classifier 예시
decision tree에서 보았던 data set을 다시 가져와보자.

테니스를 치러갈지 말지(y) 정하는 분류 문제이다. 이 문제에 대해서 특징벡터(X)하나를 뽑아보면 다음과 같다.

그리고 각각의 y값에 대한 p(y)를 구하면 아래와 같다.
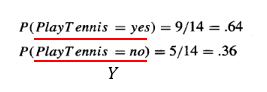
한가지 feature에 대해 각 class일 때의 likelihood를 구해보면,
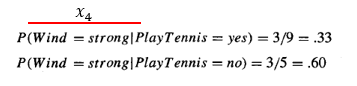
이와 같이 각각의 feature에 대해 확률을 구해서 conditional independence를 통해 곱으로 표현해보면,

이 확률을 최대로 하는 클래스를 정해야 하기 때문에 각 확률을 비교해보면, 테니스를 안치는 것(no)의 확률이 더 크기 때문에 최종 클래스 y를 테니스 안치는 것으로 결정할 수 있다.
이렇게 직접 빈도를 계산해서 확률을 구해 문제를 풀 수도 있고 다른 방식으로는 numerical variable의 distribution을 가정해 풀 수 있다.
ex)동전던지기는 binomial distribution
continuous value이면 gaussian distribution으로 가정하고 풀 수도 있다.

Laplace smoothing: overfitting을 방지한다.
만약에 앞서 보여줬던 data set이 training set이라고 하자. 그리고 새로운 data로 test해보려고 한다.
만약에 새로 가져온 data에 듣도보도 못한 새로운 값이 등장했다면? 이 경우 outlook에 foggy라는 training set에서 보지 못한 data가 등장한 것이다.

우리는 training set을 통해 확률을 계산하기 때문에 이런 foggy가 등장할 확률은 0이 된다. 이렇게 training data에 최적화 되어 새로운 data를 잘 분류하지 못하는 overfitting 문제를 해결하기 위한 방법이 필요하다.
그 방법으로 사용할 수 있는 것이 laplace smoothing이다. conditional laplace smoothing의 식을 살펴보면,

클래스의 개수에 k배를 해주어 분모에 더하고 분자에는 k를 더한다. 만약 이문제를 예시로 들면, k=1로 설정하고 클래스는 2개니까 아래와 같이 나타낼 수 있다.
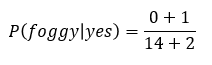
이렇게 원래 확률이 0이 될 feature에 대해 어떤 값을 더해주어 전체를 0으로 만들어버리는 불상사를 막아준다. 그리고 k에 따라 smoothing정도가 달라질 것이다. smoothing이라는 말을 이해해보기 위해 동전던지기 확률에 laplace smoothing을 적용해보면,

앞면이 나올 확률과 뒷면이 나올 확률이 k값이 커짐에 따라 차이가 점점 작아지는 것을 확인할 수 있다.
Reference
Machine Learning - Tom Mitchell
https://www.saedsayad.com/naive_bayesian.htm
https://towardsdatascience.com/naive-bayes-classifier-81d512f50a7c
'ML&DL > Machine Learning' 카테고리의 다른 글
| Regularization(정규화): Ridge regression/LASSO (0) | 2020.06.13 |
|---|---|
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |
| Bayes theorem(베이즈정리)와 MLE/MAP (8) | 2020.06.13 |
| K Nearest Neighbor(K 최근접 이웃) 원리 (0) | 2020.06.13 |
| Decision tree(의사결정나무) 원리 (0) | 2020.06.13 |



