raw데이터가 존재할 때, 그 raw data를 바로 사용할 수도 있지만 이를 가공하여 사용하기도 한다. 주어진 데이터의 특징들을 뽑아서 feature vector를 뽑아내서 이를 머신러닝모델의 input으로 사용하게 된다. 이때의 feature vector는 대체로 높은 차원을 갖는 벡터가 된다. 여러 날(day1,2,3....)이 주어졌을 때, 테니스를 할지/말지 두가지로 분류하는 문제를 통해 feature vector의 예시를 들어보면,
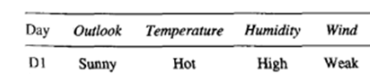
Day1의 날씨에 관한 특징 4가지를 이용해 vector를 만들면 4-dimension의 vector가 된다. 이렇게 feature engineering을 거친 데이터 set을 4D공간(space)에 뿌려놓고, 이 데이터들을 분류하는 방법인 K Nearest Neighbor(KNN/K-NN)에 대해 소개하려고 한다.
Nearest Neighbor란? 그리고 K가 무엇인가?
일단, nearest neighbor가 model을 기반으로 하는 알고리즘이 아니라는 점을 먼저 말하고 시작하겠다. 이전에 살펴봤던 decision tree의 경우나 SVM은 model-based learning을 한다는 것을 우리는 알고있다. 하지만 nearest neighbor는 instance-based learning중 하나로, 한번에 전체 instance space를 이용해서 target function을 만드는게 아닌 local하게 새 instance를 classify한다. 이게 무슨말인고하면...
별도의 model없이 데이터(instance)만을 이용해서, 새로운 데이터가 왔을 때 그때 즉석에서 주변데이터들(local하게)을 이용하여 classify를 하는 것이다.
그래서 사람들은 이런 instance-based learning을 lazy learning or delayed learning라고도 한다. 결론부터 말하자면, KNN은 가장 근접한 벡터들(local하게)과의 거리를 계산하여 어떤 class에 속하는 지 판단하는 알고리즘이다.
그것을 살펴보기에 앞서 K nearest neighbor의 다른 용도를 한번 살펴 보겠다. (classification문제에 쓰이는 nearest neighbor만 알고싶으면 여기는 스킵해도 무방하겠다.) 사실 nearest neighbor는 커널밀도추정과 함께 비매개변수적인 밀도추정에도 쓰인다. 유클리디안 D차원 공간의 알려지지 않은 확률밀도 p(x)로부터 관측값들을 추출했고 이 관측값들을 바탕으로 p(x)를 추정하려한다. 아주 작은 지역R을 바탕으로 이 구역의 확률질량은 p(x)를 R지역에 대해 적분하여 나타낼 수 있다.
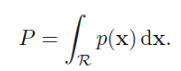
p(x)를 바탕으로 추출한 N개의 데이터포인트를 고려해보자. N개의 데이터 포인트 각각은 구역R에 포함될 확률P를 가지고 있다. 전체 N개의 데이터 포인트 중 K개의 포인트가 구역 R안에 존재할 확률은 이항분포로 나타낼 수 있다.

이 분포는 큰 N값에 대해서 평균을 중심으로 날카롭고 뾰족한 모양을 그릴 것으로 K를 아래와 같이 나타낼 수 있다.
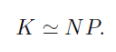
R구역이 충분히 작아서 p(x)가 대략 상수라고 하면 아래의 식을 얻을 수 있다. (여기서 V는 R구역 구의 부피)
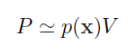
위의 두 식을 결합하면 p(x)를 구할 수 있게 된다.
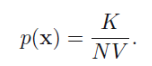
여기서 K-nearest neighbor는 K를 고정하고 그때의 V의 값을 데이터로 부터 추정하는 방법이다. 예시를 들어보면, 새로운 포인트 ○가 들어왔을 때 그 주변의 작은 구를 고려해 보도록 하자.

고정된 K개(우리가 임의로 설정하는 값)의 데이터 포인트들을 포함할 정도까지 구의 반지름을 늘릴 것이다. 결국 K는 우리가 밀도추정(뒤에선 분류)을 하기위해 포함하는 그 local한 구역에 포함되는 데이터 포인트들의 수를 의미한다. 그래서 이때의 구의 부피 V를 이용해서 밀도p(x)에 대한 추정값을 구할 수 있다. 이 테크닉을 K-nearest neighbor라고 한다. 아래의 그림은 K nearest neighbor을 이용하여 데이터의 밀도추정을 보여준다.

이를 이용해서 분류문제도 해결할 수 있게 되었는데 이는 밀도를 추정한 후 베이지안정리를 이용하면 된다. 각 클래스 Ck에 대해 NK 개의 데이터 포인트를 가지는 데이터 집합을 가정해보자.

이 상황에서 새로운 포인트 x를 분류하고 싶을 경우에 대해 생각해보자. 일단 첫째로 클래스에 상관없이 K개의 데이터 포인트를 포함하는 구를 그리자.이를 통해 V부피를 가지는 구가 되었다. 각 클래스 Ck로부터 Kk만큼의 데이터 포인트를 가지게 되었다고 하면 각 클래스에 대한 밀도를 추정할 수 있다.
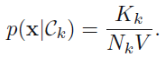
그리고 전체에 대한 밀도는 아래와 같이 추정할 수 있다.
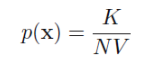
각 클래스의 밀도는 아래와 같이 추정할 수 있다.(사전밀도)

이를 통해서 사후밀도를 구할 수 있다.
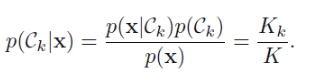
오분류의 확률을 최소화하고 싶다면 test포인트 x를 가장 큰 사후확률값(Kk/K)를 가진 클래스에 포함시키면 된다. 따라서 K개의 포인트들 중에서 가장 많은 포인트가 속해 있는 클래스에 새 포인트를 할당한다.
K-nearest neighbor의 학습? 아니 분류 방법
K-nearest neighbor가 classifiation에 사용될 때, 학습이랄게 따로 없다. 왜냐면 모델을 가지지 않기 때문. 그래서 최적의 모델을 만들기 위해 cost function을 최소화 하는 방식을 이용하지 않는다. 새로운 데이터가 들어왔을 때 그냥 '주변에 있는 나랑 제일 가까운 K개의 data point'를 이용해서 그 K개의 클래스를 다 살펴본 후, 다수결의 원칙에 의해 가장 많은 클래스쪽으로 분류된다. 이때, 나랑 제일 가깝다 = 거리가 가깝다로 해석할 수 있고, distance를 이용해서 분류를 하게 된다. 예를 들어보자.

K=3이다. 새로 들어온 포인트에서 거리가 제일 가까운 3개의 데이터포인트를 고른다. 그 후 하얀색이 2개 검정색이 1개이니까 다수결에 따라 새로운 데이터 포인트는 하얀색 클래스로 결정된다. 굉장히 간단한 알고리즘이다. K값에 따라 성능 또한 달라지는데, 아래 그림은 다양한 K값에 따라 입력공간의 분류 결과를 나타낸다.
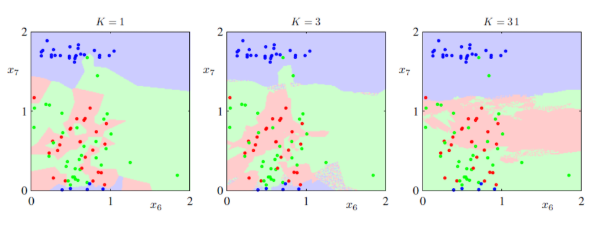
K가 작을수록, 만약 노이즈가 있을 경우 더 민감하다. 왜냐하면 내 근처에 적은 point로만 판단하는데 그 하나하나의 point에 크게 영향을 받기 때문이다. (K가 작을수록, sharp한 decision) K가 클수록, 반대로 노이즈에 덜 민감하게 된다.(K가 클수록, soft한 decision)
대부분의 K-NN은 가까운지를 판단하는 distance개념을 유클리디안거리 혹은 맨해튼 거리를 이용한다. MNISTdata에서는 cosine similarity를 이용하기도 한다. 벡터간의 거리를 구하는 두가지 공식을 보고 알고리즘 설명을 마치겠다.
1)맨해튼 거리(Manhattan distance)
L1 distance라고도 불린다. 맨해튼 전경을 위에서 바라보았을 때 마치 사각형 격자로 이루어진 것처럼 잘 정돈된 모습에서 유래되었다고 한다. 사각형 격자로 이루어진 지도에서 출발점으로부터 도착점까지 건물을 가로지르지 않고 갈 수 있는 최단거리를 구하는 공식이다.
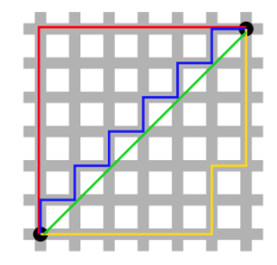
초록색을 제외하고 나머지 경로들은 건물을 가로지르지 않고 최단경로로 가는 방법들이다. 어차피 가로길이 세로길이를 다 더하면 다 같은 값이 나온다. 그래서 단순히 가로의 길이, 세로의 길이를 더하면 맨해튼 거리를 구할 수 있다.

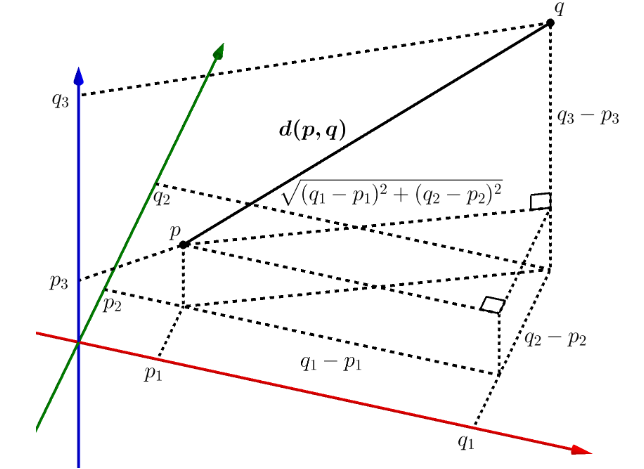
2)유클리디안 거리(Euclidean distance)
우리에게 가장 익숙한 거리공식일 것 같은 유클리디안 거리이다. L2 distance라고도 부른다.

K-nearest neighbor에서의 remark
1.모든 attribute를 기반으로 계산이 된다.
decision tree와 비교해보면, 가정을 통해서 중요한 attribute를 select하는 과정이 있었다는 것과 비교하면 큰 차이점이다. class를 구분하는데 무관한 attribute에 대해서도 계산을 진행하기 때문에 불필요한 계산량이 많아질 수 있다. 그런 단점을 극복할 수 있는 3가지 방법이 있다.
1)각각의 attribute에 다른 weight를 주는 방법.
2)training set중에서 랜덤으로 subset을 만들어 cross-validation
3)가장 덜중요한 attribute의 weight를 0으로!
2.효과적인 메모리 indexing이 중요하다.
전체 data set을 저장하고 새로운 데이터에 대해 거리를 전부 계산해야 하므로 데이터집합이 클 경우 많은 계산량을 요구한다. 이때 트리바탕의 검색구조를 만들어서 가까운 이웃들을 효과적으로 찾을 수 있도록 하여 단점을 상쇄시킬 수 있다.
Reference
Machine Learning - Tom Mitchell
Pattern Recognition And Machine Learning - Bishop
https://ratsgo.github.io/machine%20learning/2017/04/17/KNN/
'ML&DL > Machine Learning' 카테고리의 다른 글
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |
|---|---|
| Naive bayes classifier(나이브 베이즈 분류기) 원리 (0) | 2020.06.13 |
| Bayes theorem(베이즈정리)와 MLE/MAP (8) | 2020.06.13 |
| Decision tree(의사결정나무) 원리 (0) | 2020.06.13 |
| SVM(Support Vector Machine) 원리 (5) | 2020.06.12 |



