분류(classification)과 회귀(regression)문제를 풀기 위한 다양한 종류의 머신러닝 모델이 존재한다.
단일모델을 사용하는 대신 여러 모델을 특정방식으로 조합하면 성능이 더 나아지는 경우가 있다.
1)위원회방식(committees): L개의 서로 다른 모델들을 훈련해서 각 모델이 내는 예측값의 평균을 통해 예측을 시행하는 방식
2)부스팅방식(boosting): 여러모델을 순차적으로 훈련하는데, 각 모델을 훈련하기 위한 오류함수는 그 이전 모델결과에 의해 조절
3)여러 모델 중 하나의 모델을 선택해서 예측을 시행하는 방법 ex)decision tree(의사결정트리)
오늘은 이 중에서 decision tree에 대해 알아보도록하자.
Decision tree란?
우리가 알고있는 머신러닝 모델들은 함수로 생각할 수 있다. input이 들어갔을 때, 원하는 output(분류라던가 회귀)이 나오도록 하는 바로 그!!모델을 찾는 것이 중요하다.

decision tree(의사결정트리)는 순차적으로 질문을 던져서 답을 고르게 하는 방식으로 의사결정을 하는 머신러닝모델이다. 쉽게 말하면 일종의 스무고개와 같겠다.
예를들어, 의학진단의 경우 환자의 질병을 예측하기 위해 첫번째로 '체온이 어떤 임계값보다 높습니까?'라고 물어볼 수 있을 것이다. 만약 그렇다고 대답한다면 다음으로 '혈압이 어떤 임계값보다 낮습니까?'라고 물을 수 있을 것이다. 이렇게 일련의 질문에 의해 점점 분류되어 결국 진단결과로 질병이 걸렸는지/안걸렸는지를 판단할 수 있을 것이다.
이런 스무고개 놀이를 트리구조를 이용하여 구현할 수 있다.

그래서 우리는 이를 의사결정을 하는 트리다~해서 decision tree라고 부른다. decision tree는 분류(classification)와 회귀(regression)문제를 모두 해결할 수 있다. 이에 대해선 뒤에 다시 설명하도록 할 것이고 예시에선 분류문제를 살펴볼 것이다. 트리기반 모델들로는 CART(classification and regression tree), ID3와 C4.5 등이 존재한다.
여기서 언급하는 트리는 무엇인가?

나무를 거꾸로 뒤집은 모양으로 생각할 수 있다. 뿌리(root)노드로 부터 노드들이 가지(branch)들로 노드가 연결되어 있고 마지막 노드들이 잎(leaf)처럼 달려있는 자료구조를 뜻한다. 이런 트리구조를 이용해서 하나의 예시를 통해 decision tree를 구성해보자! 우리는 2주 동안 하루의 날씨,습도,바람을 조사해서 그 특성들에 따라 day by day로 테니스를 하러갈지 말지를 정하고 싶다. 그렇다면 이런 decision tree를 만들 수 있다.

테니스를 하러 갈지말지는 (테니스 한다=yes, 테니스 안한다=no) 이진분류(binary classification)문제이다.
그러므로 classfication에 사용된 decision tree가 되겠다. 각 구성요소가 decision tree에 사용되는지 한 번 정리해 보자.
1)root node~leaf node전까지의 node: input데이터를 분류할 수 있는 특성(attribute,feature) ex)humidity
2)branch: 그 feature가 가질 수 있는 값(value) ex)high,normal
3)leaf node: 분류결과(output)
그래서 leaf node를 제외한 node들에 attribute들을 잘 배치하여 attribute들이 가질 수 있는 값에 따라 분류를 하게 되는 것이다. 아까 살펴본 머신러닝 기본 틀을 decision tree 모델에 맞게 다시 표현해보면 아래의 그림처럼 될 것이다.

input data는 특징벡터로 나타나고, decision tree를 통과하여 결과로 yes/no 둘 중 하나로 분류되었다. 하나의 decision tree를 만들어 봤지만, 특성(attribute)을 어떻게 배치하느냐에 따라 여러 decision tree를 만들 수 있을 것이다. 어떤 질문을 먼저 하느냐에 따라 분류성능이 더 좋을 수도 있고 더 나쁠 수도 있겠다. 그러므로 어떤 노드에 어떤 attribute를 선택해 넣을지가 중요한 것이다. 쉽게 말해 어떤순서로, 어떤 배치로 질문을 할 지 정하는 것이 decision tree의 핵심이 된다.

이런식의 data set을 예시로 들 수 있겠다. 파란상자는 input data들을 나타내고 y는 그 데이터에 따른 정답지를 나타낸다. 이를 이용해서 어떻게 모델을 최적화할지!!( 어떤 노드에 어떤 attribute를 선택해 넣을지 )의 알고리즘을 알아보겠다.
Cost function: information gain (feat. entropy개념)
Decision tree에서는 information gain이라는 statistical based property를 measure로 사용한다. information gain은 tree가 자라나면서 각각 step에서 feature후보들중 어떤 feature를 선택할지 정할때 이용된다. information gain을 한국말로 하면 정보획득량이다. 정보하면 또 떠오르는 중요한 개념인 entropy를 알아보자.
정보이론에서 entropy(엔트로피)란 우리가 가지고 있지 않은 정보의 양을 의미한다. 즉, 우리가 얼마나 어떤 시스템에 대해 혹은 변수에 대해 모르고 있는지, 얼마나 실제 관측이 우리를 놀라게 할 수 있는지에 대한 값이다.

위에 데이터와 아래의 데이터를 비교해보자.
1)위의 데이터는 변화가 없이 모두 채워진 원이다. 그래서 다음에 나올 데이터도 채워진 원이 나올 것이라고 쉽게 예측할 수 있다. 즉 불확실성이 낮다고 볼 수 있다. 이런 경우에는 얻을 정보량이 작다고 한다. 즉 얻을 것이 없고 놀랄 것도 없는 것이다. 이렇게 순도가 높은 상태는 엔트로피가 낮은 상태가 된다. 이렇게 모든 데이터가 같은 값을 가지는 경우 entropy가 0이 된다.
2)아래의 데이터는 중간중간 속이 빈 원이 존재한다. 그래서 결과를 예측하기가 더 어려워진다. 이럴 경우 불확실성이 높다고 할 수 있다. 그러므로 다음에 나올 데이터에 우리가 더 놀라게 될 것이다. 이런 경우 얻을 정보량이 많다고 한다. 이렇게 불순도가 올라갈 수록 엔트로피가 높은 상태가 된다.
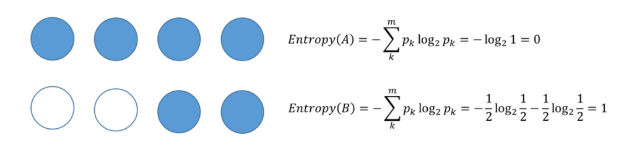
극단의 상황으로 갔을 때, 모두 같을 가지면 순도가 높고 불확실성이 최소이고 얻을 정보는 없어지므로 엔트로피는 0이 된다. 그리고 완전 반반의 상황일 때는 불순도가 가장 높고 불확실성이 최대이고 얻을 정보가 많아지므로 엔트로피가 1이 된다.

채워진원을 + 비워진원을 -라고 할때, 채워진원의 확률에 따라 엔트로피그래프를 구해보면 위의 그래프가 된다. 이번엔 이런 binary classification에서 entropy의 개념을 알아보겠다.

위와 같은 데이터가 존재한다고 하자. 전체 주황박스를 A라고 하고 R1과R2 두개의 부분집합으로 나눈다고 가정한다. 처음 전체 데이터 A에 대한 entropy를 구해보면,

여기서 R1과 R2로 나눈 후 두 개의 영역에 대한 엔트로피공식을 이용해 A의 entropy를 다시 구해보면,

처음 영역을 분할하지 않았을 때보다 엔트로피가 0.95에서 0.75로 낮아졌다. (=불확실성 감소=순도 증가=entropy가 낮다) 이런 방식으로 엔트로피가 낮아지는 방향으로 학습을 진행하게 된다.

이제 우리는 위와 같은 decision tree를 만들때 불순도를 줄이는 방식 즉 점점 아래 노드로 갈 수록 데이터의 entropy가 낮아지는 방식으로 feature들을 어느 노드에 배치할지 정할 수 있을 것이다!
entropy를 이용해서 decision tree의 information gain을 구할 수 있다. ID3방식의 information gain는 아래와 같이 정의할 수 있다.

사실 분기가 나눠지지 않은 전체 엔트로피는 항상 값이 고정되어있는 상수이기 때문에 뒤에 엔트로피계산이 전부라해도 무방하다.
Decision tree model의 학습: greedy algorithm
Decision tree는 information gain이라는 measure를 이용해서, 지금 현재상황에서 가장 information gain이 높은 attribute를 현재노드로 선택해나가는 greedy algorithm을 통해 학습을 한다. 아까의 예시로 다시 돌아가서, 계산을 직접 해보자.

위와 같은 데이터셋이 있을 때, yes를 +로 no를 -로 정의한다면, +는 9개고 -는 5개가 된다. 일단 wind라는 feature를 이용했을 때의 information gain을 구해보자.

위의 방법으로 humidity라는 feature를 이용했을 때 information gain도 구할 수 있다.

둘을 비교해보면, hummidity라는 feature를 이용해서 S집합을 분류할 때가 wind라는 feature를 이용해서 분류할때보다 더 information gain이 크다는 것을 알 수 있다. 같은 방식으로 모든 feature에 대해 information gain을 구해보면 아래와 같다.

여기서 가장 information gain이 큰 outlook을 가장 root노드로 둔다.

그다음 이제 분류된 데이터들의 entropy를 구하고 overcast의 경우 entropy가 0이므로 stop! 나머지 sunny와 rain은 또 그다음 노드의 attribute를 어떤 것으로 정할 지 information gain을 구해본다. 그래서 sunny같은 경우 위의 그림에서 볼 수 있듯이 가장 information gain이 큰 hummidity로 다음 노드의 attribute를 정한다.
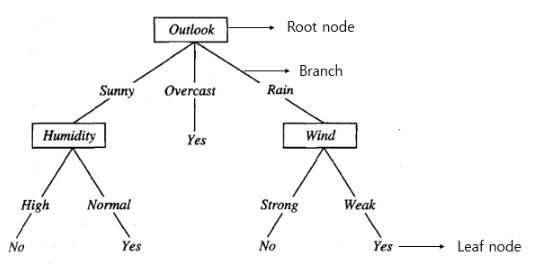
이 방식을 쭉해서 처음에 봤던 이 decision tree를 완성할 수 있다. key idea of tree learning은 가장 큰 information gain을 가지는 attribute를 가장 root에 가깝게 하는 것이다!!!(중요중요)
가지치기(Pruning):overfitting 방지
decision tree의 분기수가 증가할 때 처음에는 새로운 데이터에 대한 오분류율이 감소하나 일정수준 이상이 되면 오분류율이 되레 증가하는 현상이 발생한다. training accuracy가 계속 올라가면서 test accuracy가 같이 올라가다가 일정수준 이상이 되면 떨어지는 현상. 이를 overfitting현상이라고 한다. =>trainning data는 잘 설명하지만 generalize가 잘 안된다.

기본적인 decision tree는 inductive bias가 없기 때문에 이런 overfitting 현상이 생긴다. (inductive bias는 모델이 너무 training data에 맞게 설계되어 generalize되지 못하는 문제를 해결하기 위해 임의로 가해주는 constraint를 뜻한다.) 아래의 그림을 통해 보면 모델(hypothesis(가정))이 학습을 거칠 때, 차수가 너무 높아지면, 원래 데이터를 표현하는 초록색 그래프를 잘 표현하는 것이 아닌, training데이터에 관해서만 딱 맞는 빨간 그래프를 생성한다.

이럴 경우 너무 variance가 높아지게 된다. 그리고 전체 데이터셋을 표현하는 초록그래프와 많이 달라진다.

이때 M=0이라는 bias를 걸어주면 굉장히 간단한 모델을 만들 수 있다. 이런식으로 M값을 조절해서 전체데이터를 잘 표현할 수 있는 generalized 모델을 찾는게 중요하다. 그니까 쉬운말로 bias는 임의로 모델에 가하는 제약사항같은 것.
(**여러 모델들에 쓰이는 inductive bias기법들)

- 그러므로 training set의 error는 항상 zero이다.
- infinite variance를 가진다.
더 간단한 트리를 만들기 위해 bias를 가질 필요가 있다.(depth를 고정할 수도 있고, leaves를 고정할 수도 있다.)
또다른 방법으로는 overfitting문제를 해결하기 위해 가지치기(pruning)를 하는 것이다. 말그대로 전체 트리를 만든다음 오분류율이 다시 증가하는 시점에서 적절히 가지를 쳐주는 것을 말한다.
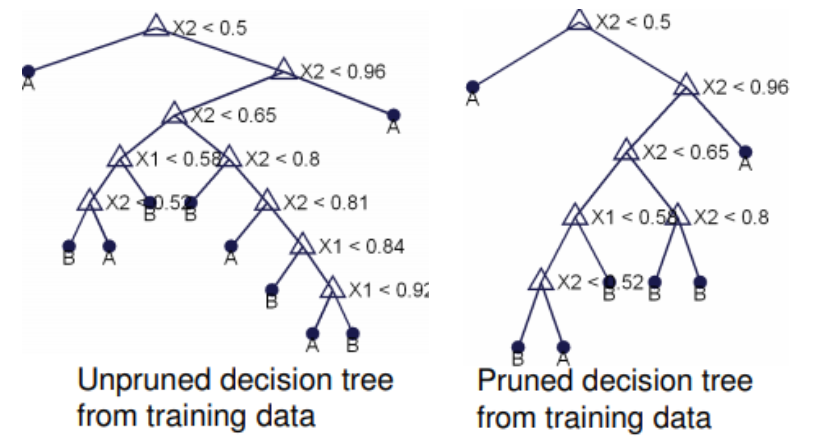
방법으로는,
1)test data를 추가로 넣어본다(validation set).
이 방법은 일단 전체 tree를 만든 후 leaves에서부터 시작해서 reculsive하게 split을 제거하는 것이다. test data의 성능을 검증한 후 split을 제거하면 성능이 올라간다면 그때 tree를 prune한다.

2)statistical significance test를 해본다. (chi-square test)
모든 leaf node의 순도가 100%인, entropy가 0인 상태를 full tree라고 하는데, 우리가 만든 이 tree가 문제가 되는 이유는 information gain이 높아지면 split하는 방식만 이용하고 entropy의 변화가 statistically significant한지는 살펴보지 않았기 때문이다. '통계적 중요성'을 기반으로 chi-square을 계산할 수 있는데 이에 대해 알아보자. 여기서 빨간점이 class A, 초록점이 class B이다.

데이터가 Left chilld로 가는 비율은 아래와 같다.

그리고 class A와 B가 각각 left child node에서 expected num이 아래와 같이 나온다.

NA 와 NB가 NA' 와 NB'로부터 충분히 다르다면? 둘의 차이가 커진다. 그럼 statistically significant. 그대로 split! NA 와 NB가 NA' 와 NB'와 유사하다면? 둘의 차이가 작아진다. 그럼 statistically significant하지 않음. split하지 말자!

그것을 식으로 위와같이 정리할 수 있다. 이 값이 작으면 information gain이 커져도 split하는게 중요하지 않음... Prunning하자.(분기하지 말자.) "Small (Chi-square) values indicate low statistical significance" 이 값이 크면 분기하자. 위의 식을 조금 더 일반화하여 정리하면,

이를 chi-square이라고 부른다. 여기서 threshold를 설정해서 prunning할지 말지 정할 수 있다. t를 threshold라고 했을 때,
Lower t bigger trees (more overfitting).
Larger t smaller trees (less overfitting, but worse classification error).
Chi-square값을 이용해서 P-value라는 개념을 도입할 수도 있다.
Chi-square값을 이용해서 확률값으로 P-value를 구할 수 있다.
Chi-square가 커질수록 P-value는 값이 작아지는 것을 그래프로 확인할 수 있다.

이를 이용해서 MaxPchance라는 threshold값을 줘서 그 threshold보다 큰 P-value를 가지면 prunning해야한다. 더 많이 prunning(=simpler decision tree를 만든다)하기 위해선 MaxPchance를 낮춰야 된다.
3)비용함수 이용
full tree를 생성한 후 적절한 수준에서 분기를 합치는데 이런 가지치기도 비용함수로 만들어 최적의 분기를 찾을 수 있다.

이 비용함수를 최소화하는 분기를 찾으면 되겠다.
CC(T)=의사결정나무의 비용 복잡도(=오류가 적으면서 terminal node 수가 적은 단순한 모델일 수록 작은 값)
ERR(T)=검증데이터에 대한 오분류율
L(T)=terminal node의 수(구조의 복잡도)
Alpha=ERR(T)와 L(T)를 결합하는 가중치(사용자에 의해 부여됨, 보통 0.01~0.1의 값을 씀)
Reference
https://blog.naver.com/angryking/221206754322
https://ratsgo.github.io/machine%20learning/2017/03/26/tree/
https://blog.naver.com/ehdrndd/221158124011
http://www.cs.cmu.edu/afs/cs.cmu.edu/academic/class/15381-s06/www/DTs2.pdf
'ML&DL > Machine Learning' 카테고리의 다른 글
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |
|---|---|
| Naive bayes classifier(나이브 베이즈 분류기) 원리 (0) | 2020.06.13 |
| Bayes theorem(베이즈정리)와 MLE/MAP (8) | 2020.06.13 |
| K Nearest Neighbor(K 최근접 이웃) 원리 (0) | 2020.06.13 |
| SVM(Support Vector Machine) 원리 (5) | 2020.06.12 |



