Unsupervise learning, 그니까 label이 없는 data set을 학습시키는 방법중에 clustering(군집화)이라는 기법이 있다. K개의 clustering point(cluster center)를 잡고 데이터 집합에서 가장 가까운(거리개념) 애들끼리 같은 class를 주는 방식이다. 그리 어렵지 않은 알고리즘이지만 성능이 좋은 편이다. 이 알고리즘도 일종의 EM알고리즘이 되는데 이에 대해서는 추후에 살펴보도록 하고, 이번 포스팅에서는 간단히 K-means clustering알고리즘을 알아보도록 하자.
K-means가 무엇인가?
일단 기본적으로 몇개의 cluster로 묶을 지, 원하는 cluster의 개수를 K로 설정해준다. 그리고 갯수 K개에 대하여 거리가 가까운 놈들끼리 묶어주기만 하면된다. 여기서 cluster의 중심이 되는 data point를 cluster center라고 부르는데, 얘를 K개 설정해줘야한다. 이때 cluster center는 알고리즘을 거듭해나감에 따라 해당 클래스의 평균을 내는 방식으로 update되기때문에 K-means clustering(K-평균 군집화)이라는 이름이 붙게된 것 같다.
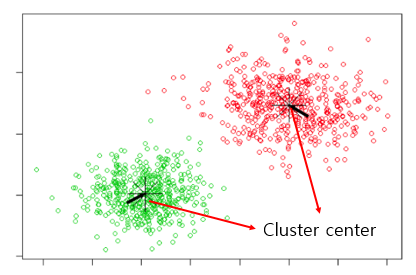
여기서는 K=2기 때문에 cluster center가 2개 존재하고, 거리가 가까운 놈들끼리 뭉쳐있는 것을 확인할 수 있다. scikit learn에서 K만 지정해주면 쉽게 구현할 수 있다.
K-means clustering 알고리즘
k-means clustering의 알고리즘을 아래와 같이 나타낼 수 있다.

cluster center가 정해졌을 때, 각 cluster center에 대해서 data point와의 거리를 계산한다. 그리고 거리가 가장 짧은 cluster의 class로 배정한다. 이런 과정을 다 거쳐서 모든 data point의 class가 정해졌다면, 정해진 class에 해당하는 data point를 이용해서 그 class의 평균을 구해 cluster center를 업데이트한다.
말로 설명하면 잘 와닿지 않으니 예시를 들어 보겠다.
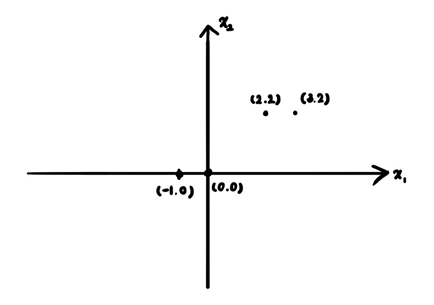
2차원 데이터포인트 4개가 존재한다고 하고, K=2 즉, 2개의 cluster를 만들고싶다고 하자. 우리는 눈으로 딱보면 어떻게 두개로 나눠야할지 보이지만,,, k-means clustering으로는 어떻게 두 cluster로 나누는지 보겠다.
1. 첫번째 iteration
1) 임의의 initial clustering center를 설정한다.

2) clustering center에 대해 모든 data의 거리를 계산한다.(여기서 나는 유클리디안 거리의 제곱을 이용)
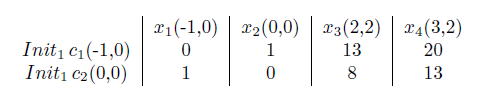
3)거리가 가까운 cluster center의 class로 각 data point를 배정해준다.


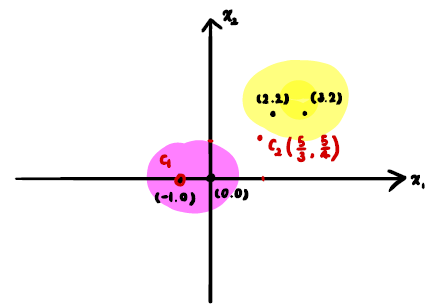
4)class가 업데이트된 data point에 대해 다시 cluster center를 계산한다.


2. 두번째 iteration
1) 1번째 iteration에서 정한 cluster center에 대해 모든 data의 거리를 계산한다.

2)거리가 가까운 cluster center의 class로 각 data point를 배정해준다.

3)class가 업데이트된 data point에 대해 다시 cluster center를 계산한다.


3. 세번째 iteration
1) 2번째 iteration에서 정한 cluster center에 대해 모든 data의 거리를 계산한다.
2) 모든 data에 대해 class가 바뀌지 않으므로(수렴했다!!) 끝낸다.
K-means clustering과 EM알고리즘
앞서 살펴본 k-means clustering알고리즘은 사실 EM알고리즘으로 설명할 수 있다. k-means clustering 알고리즘에서 우리가 찾고싶은 것은 2가진데,
1)최적의 cluster center 2)각 data point가 어디에 속하는지 이다.
이렇게 여러가지 해를 동시에 찾기 어려울 때, E(expection,기댓값)과정과 M(maximization)과정을 거쳐 해를 찾게된다. 이 과정을 간단히 말해보자면,
1)을 고정해놓고 최적의 2)를 찾은 후, 2)를 고정해놓고 최적의 1을 찾는 과정을 반복하는 것이다.
EM알고리즘을 clustering에 적용하는 방식으로 풀이를 해보고 마치겠다. objective function(목적함수)은 아래와 같이 정의하도록 한다.

이를 뒤틀림척도라고 부르고 할당된 cluster center 뮤벡터로 부터의 거리의 제곱을 합한 것이다. 이 때, 목적함수 J를 최소화하는 1)최적의 cluster center 2)각 data point가 어디에 속하는지 를 찾는 것이다! 아래의 형광펜부분을 찾는 것!


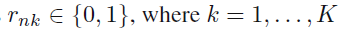
클래스를 rnk벡터로 표현할 수 있다고 하자. (one-hot-encoding)
(n번째 data sample이 k번째 클러스터에 속하는 것을 표현)
Estep에서는 앞서 정의한 objective function을 최소화하는 j(클래스,클러스터)를 찾는것이 목표가 된다.
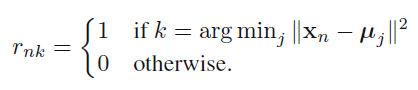
그렇게 rnk가 모두 정해지면,
Mstep에서는 정해진 rnk를 대입하여 cluster center 뮤에 대해 objective function을 미분해서 0이되는 뮤를 찾으면 된다.
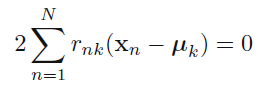
뮤에 대해 정리해보면, 앞서 봤던 평균내는 식이 나온다.
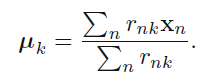
Reference
Bishop - Pattern Recognition And Machine Learning
GIST 최종현교수님수업
https://ratsgo.github.io/machine%20learning/2017/04/19/KC/
'ML&DL > Machine Learning' 카테고리의 다른 글
| HMM(Hidden Markov Model, 은닉마르코프모델) 원리 (0) | 2020.06.13 |
|---|---|
| GMM(Gaussian Mixture Model,가우시안 혼합모델) 원리 (4) | 2020.06.13 |
| Kernel/Kernel trick(커널과 커널트릭) (4) | 2020.06.13 |
| Regularization(정규화): Ridge regression/LASSO (0) | 2020.06.13 |
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |



