저번학기에 머신러닝과딥러닝수업을 들으면서 배웠던 내용을 정리하면서 하나씩 포스팅을 한게 꽤 많이 쌓였다. HMM같은 경우에는 따로 수업에서 다루지는 않았지만, sequential한 데이터의 classifiation에서 많이 쓰이던 모델이여서 한번 정리해보려고 한다. 이곳과 이곳을 참고해 정리한 내용이다.
음성 = sequential data이므로 HMM을 모델로 쓴 예전논문이 많은 것 같다. 하지만 한번도 처음부터 끝까지 공부해본적은 없다...하하하 사실 처음보면 한눈에 어려워서 포기하고싶은 HMM..... 그래도 차근차근 정리해보겠다!! 마르코프모델이 무엇인지에서 출발해서 HMM으로 어떤문제를 풀 수 있는지까지 다뤄보자.
MM(Morkov Model)이란?
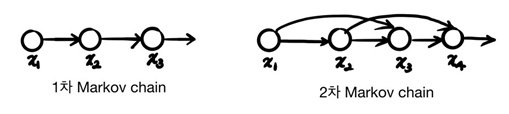
Markov model의 핵심은 현재의 observation이 바로 이전의 state에 의해서만 결정된다는 것이다. 그러므로 이전의 모든 state를 다 볼 필요 없이 이전 state만 보면 된다는 것이다. 만약 1차 마르코프모델이라면 바로이전 state만, 2차 마르코프모델이라면 두스텝 전까지 보는 것이다(영향을 받는다).
마르코프모델도 확률모델로 확률이 제일 크게 되는 쪽으로 미래값을 예측할 수 있다.

역시 예시로 공부하는 것이 잘 와닿는다. 날씨예측문제를 예로들어 markov model을 이해해보자.
1)state: 날씨
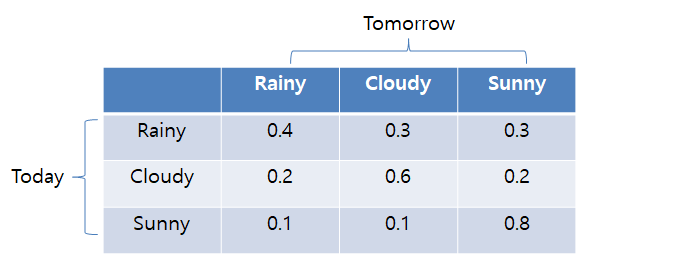
2)observable state(관측가능한 상태): {Rainy, Cloudy, Sunny}
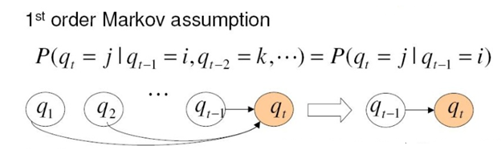
3)가정: 오늘날씨(current state)는 어제날씨(previous state)에만 영향을 받는다. (1차 마르코프모델)
4)state transition확률: 각 노드에서 나가는 transition확률을 모두 더하면 합이 1이다.
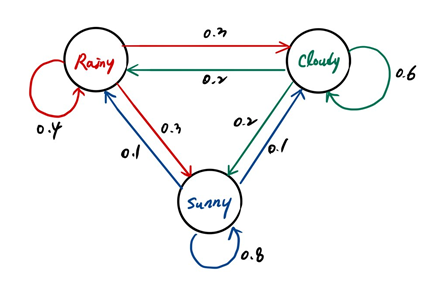
4)Markov Model 도식화:
5)풀 수 있는 문제:
문제1) 과거의 관측치가 아래와 같을 때, 다음에 나올 날씨는 무엇일까?
sunny→sunny→cloudy→rainy→sunny→?
각 state가 T=t(현재) 나올 확률(1차마르코프모델가정을 통해 바로 이전 상태에 대한 조건부확률이용)을 계산해서 제일 큰 확률을 갖는 state로 결정한다. 하지만 실제로 풀려고 하는 문제는 이보다 더 복잡한 문제이다. 문제2를 통해 MM으로 풀 수있는 다른 문제를 살펴보자.
문제2)오늘 날씨가 sunny인 경우, 다음 7일간의 날씨 변화(state sequence)가 아래와 같을 확률은?
sunny→sunny→rainy→rainy→sunny→cloudy→sunny
우리는 단지 과거의 관측치를 통해 오늘 날씨를 예측하고 싶은게 아니라, 미래에 어떤 관측치들이 나올지 예측하고 싶은 것이다. 이는 sequence probability를 이용해 계산할 수 있다. sequence probability를 계산하는 식은 아래와 같다.

이를 문제2에 대입해보면,
S1=rainy, S2=cloudy, S3=sunny이고, 여기서 조건부로 model이 걸려있는데 이건 markov model의 전제가 되는 조건들이 들어간다. 이를테면 state transition probability와 몇차 markov모델인지... 여기선 1차로 가정했다.
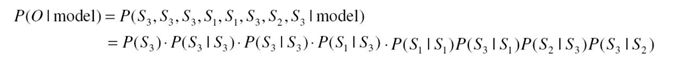
계산최적화에 대해서는 따로 다루지 않겠다. MM은 대략적 개념을 알고 HMM에 대해 더 자세히 알아볼 것이기 때문이다..... 마지막으로 마르코프모델의 종류를 언급하고 넘어가겠다. 마르코프모델은 state transition(상태천이)의 형태에 따라 날씨모델과 같은 에르고딕 모델과 음성인식에 많이 적용되는 좌우모델이 있다.
왜 Hidden인가?
HMM에서 hidden이라는 말이 나오는데 무엇이 도대체 숨겨져있다는 뜻일까? 여기서 숨겨져있는 것은 아까 MM에서의 state(상태)를 뜻한다. 우리가 알고싶은것은 state(상태)인데(!!!) 그게 숨겨진 상황을 말한다.

아까 들었던 날씨예측에서 생각해보면, 날씨를 예측해야되는데 과거 날씨들을 알 수 없는 상황인 것이다. 예를들면 우리가 어느 외딴집에 갇혀있어서 날씨를 아는 방법이 매일 밥을가져다주는 감시자가 우산을 가지고있는지 아닌지로 확인할 수 있다고 하자. 그럼 우산을 가지고있는지 아닌지가 관측치(observation)이 되는 것이다.
HMM(Hidden Markov Model)
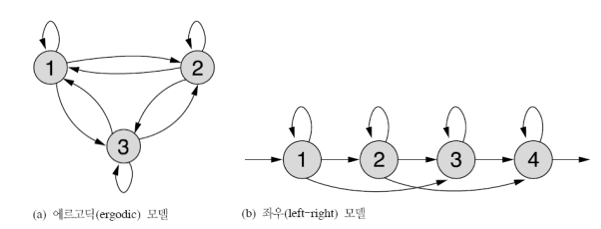
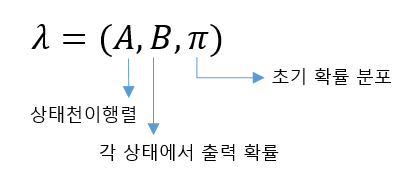
HMM은 3가지의 파라미터로 구성되어있다. 이 3가지파라미터를 찾으면 task에 맞는 HMM을 찾았다고 할 수 있다.
MM과 HMM의 차이는 수식을 보면 보다 명료하게 받아들일 수 있다. 날씨 마르코프과정을 떠올려보자,
MM같은 경우에는 날씨가 관측이 가능하므로, 어떤 날씨열
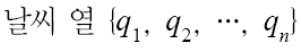
이 관측될 확률은 결합확률(joint probability)로 바로 표현할 수 있다.
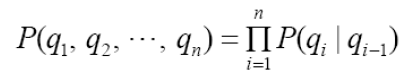
HMM같은 경우에는 날씨는 직접 관측이 불가능하며 은닉(hidden)되어 있다. 그러므로 이는 감시자가 우산을 가져왔는지 아닌지 우산열의 관측값을 통해서만 추정할 수 있다.
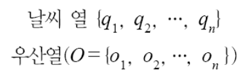
이를 조건부확률로 표현할 수 있다.
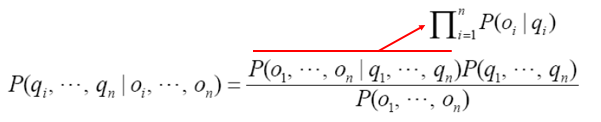
날씨열과 우산열은 모든 i에 대해 독립이므로 빨간줄 윗부분으로 변환할 수있다. 그리고 위의 조건부확률 식처럼 좌변의 값을 우리가 알 수 없기 때문에 우변의 likelihood값이 이와 비례한다.
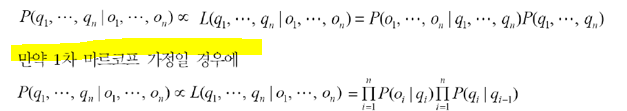
HMM에 대한 3가지 문제가 있고 이에 대해 뒤에 나오는 각 파트에서 소개하도록 하겠다.
1)확률평가(probability evaluation)문제 → forward(전향)과 backward(후향)알고리즘으로 해결

주어진 모델에서 관측열이 출력될 확률이 얼마인지 효과적으로 계산할 수 있어야한다. 그 확률값에 따라 최적의 모델을 다수의 모델로부터 선택할 수 있기 때문이다.
2)최적의 상태열(optimal state sequence)를 찾는 문제 → Viterbi algorithm으로 해결

관측열로부터 정확한 상태열을 알아내는 것은 어렵겠지만, 가장 최적의 숨겨져있는 상태열을 찾아내고싶을 때 어떻게 찾을지에 대한 문제이다.
3)파라미터 추정(parameter estimation)의 문제 → EM알고리즘

어떤 모델에서 발생한 관측열의 집합이 주어질 때, 이 관측열을 가장 잘 설명하는 모델의 파라미터들을 어떻게 최적화하여 구할지의 문제이다. 모델에 대해서 관측열의 출력이 최대가 되도록 모델의 파라미터를 조절하는 문제이다. HMM응용분야에서 성능을 결정하는 중요한 사항이다.
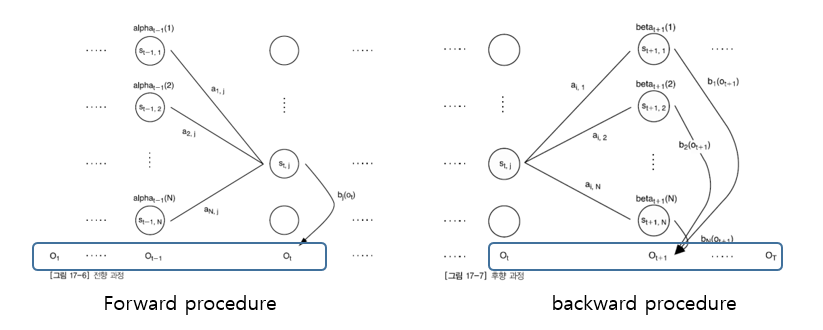
Forward algorithm & Backward algorithm
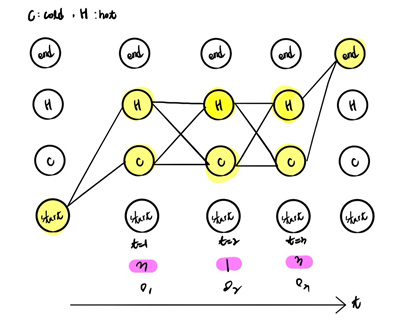
첫번째 문제는 모델이 주어져있을 때 관측치가 나올 확률인 Likelihood(우도)를 구하는 문제이다. 한가지 예시를 통해서 likelihood를 그냥 막바로 구해보고 왜 forward알고리즘을 사용하는 지 보이겠다. 아이스크림 소비기록만을 가지고 날씨를 추정하려고 할 때, 은닉마르코프모델을 도식화하면 아래와 같다.
observation O={1,2,3} :아이스크림 섭취 개수
state Q={HOT, COLD} :날씨


여기서 A는 state transition probability B는 emission probability이다.
likelyhood를 모델이 주어졌을 때 관측치가 나올 확률로 두고 문제를 풀어보자. 아래와 같이 식을 쓸 수 있다.
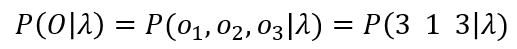
이 관측치가 state의 모든 경우에 대해서 계산되어야 하므로 이에따라 모든 경우를 더해서 계산할 수있다.
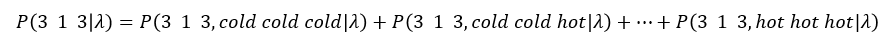
여기중에서 하나를 계산해보면,(앞서구한 A와 B를 통해 계산가능)
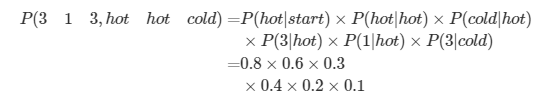
이를 모두 계산하면 전체 가짓수가 23(NT)가 된다.(N이 state T가 time step) 이걸 다 계산하는 것은 비효율적인데, 중복되는 계산이 많기 때문이다. 이를 dynamic programming 기법을 통해 빠르게 계산할 수 있다.
이런 알고리즘들이 나오게 된 것이라고 생각하면 된다.
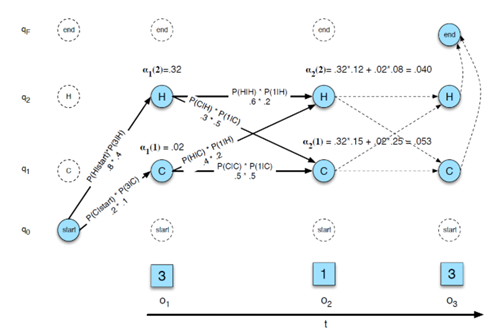
그래서 우리는 각 노드에서 forward probability라는 변수를 두고 반복되는 값을 저장해서 사용할 수 있다. t번째 계산을 할 때, t-1번째 계산이 반복적으로 사용되는 것을 알 수 있다. 그래서 이를 저장후 다시 사용할 수 있는 것이다.
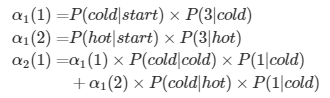
일반화하여 아래와같이 표현할 수 있다.
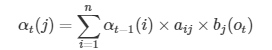
여기서 이 at(j)가 forward probability를 뜻한다. 이때 t가 현재 time step이고, j가 j번째 상태를 뜻한다.
그리고 at(j)는 이때 가능한 모든 경우를 모두 합친 확률이다. 그러므로 t=T일때 모든 state의 forward probability를 합하면 마지막 likelihood를 구할 수 있다.
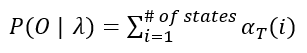
여기서 이런 likelihood를 forward 과정을 통해서도 구할 수 있고, backward과정으로도 구할 수 있는데 backward과정은 이와 유사하므로 생략하고 넘어가겠다.(첨부해둔 ppt파일에 세부내용을 확인할 수 있다.)
Viterbi algorithm: Sequence 예측하기
이번엔 관측치로부터 가장 최적의 숨겨져있는 상태열을 찾아내고싶을 때 어떻게 찾을지에 대한 문제이다.
어떻게 가장 그럴듯한 상태열을 찾을수 있을까? 각 시간 t에서 개별적으로 가장 그럴듯한 상태 qt를 찾으면 된다. 하나의 최적 상태열의 경로를 찾는 방법은 사후확률P(q|O,λ)를 최대화하는 경로를 설정할 수 있다. (λ:HMM모델)
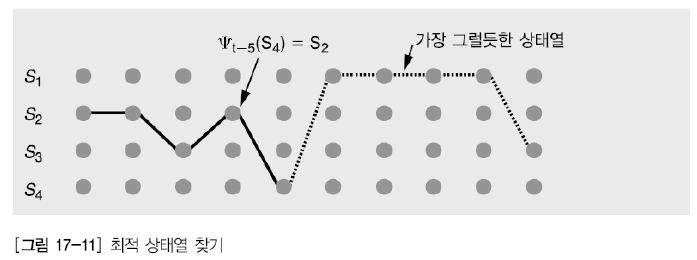
여기서 사후확률을 forward-backward변수로 정의한다.
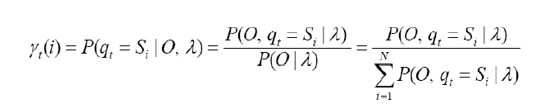
이는 forward probability와 backward probability의 곱과 같으므로, 아래와 같이 쓸 수 있다.

이를 최대화 하는 상태 qt를 찾아서 모든 t에 대해 모으면 최적의 상태열을 구할 수 있다.
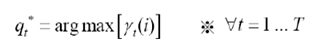
HMM의 파라미터 학습: Baum-Welch 재추정 알고리즘
이또한 EM알고리즘으로 추정할 수 있다.

1) Expectation단계
모델의 파라미터를 고정시키고 관측치를 바탕으로 forward probability, backward probability를 계산한다.
이를 이용해 forward-backward변수와 ξ를 업데이트한다.

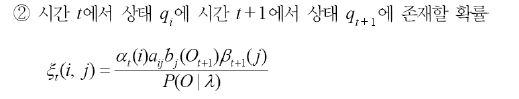
2) Maximization단계
이를 통해 모델 파라미터를 업데이트한다.

'ML&DL > Machine Learning' 카테고리의 다른 글
| MAP와 Regularization(Ridge/Lasso)의 관계 (0) | 2025.12.11 |
|---|---|
| GMM(Gaussian Mixture Model,가우시안 혼합모델) 원리 (4) | 2020.06.13 |
| K-means clustering(K-평균 군집화) 원리 (0) | 2020.06.13 |
| Kernel/Kernel trick(커널과 커널트릭) (4) | 2020.06.13 |
| Regularization(정규화): Ridge regression/LASSO (0) | 2020.06.13 |



