개인공부용 블로그로 이곳의 내용에 개인적으로 추가정리하였다. 가우시안 분포는 데이터를 분석하는 데 있어서 중요한 여러 성질을 가지고 있지만, 실제 데이터셋을 모델링 하는데에는 한계가 있다.(어떻게 모든 데이터가 종모양분포를 띄겠나...) 그래서 나오게 된 것이 Gaussian Mixture Model(GMM)인데, 여기서 mixture model이라는 것의 뜻은 기본분포를 선형결합해서 만든 분포라는 뜻이다. 그러므로 GMM은 가우시안분포를 선형결합하여 만들어진 분포를 뜻한다. (이런식으로 모델을 딱 가정해버리면 모델에 들어가는 파라미터를 찾는 식으로 밀도를 추정하게 된다. 만약 모델을 가정하지 않는다면, non-parametric하게 밀도를 추정하게 된다. ex.커널밀도추정)

예를들어 위의 오른쪽 그림과 같은 분포는 가우시안분포 하나만으로 표현하기 어렵다. 그렇기 때문에 하나의 가우시안분포로 표현하기 어려운 데이터는 가우시안분포를 여러개 합쳐서 표현할 수 있다.
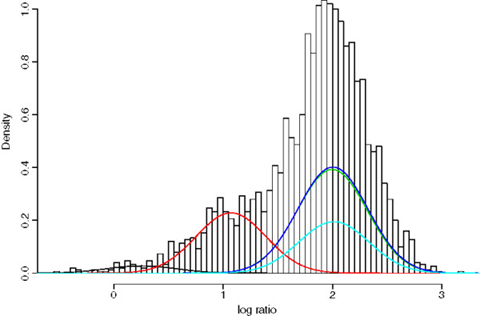
이제 GMM에 대해 formal하게 살펴보고 GMM에 EM알고리즘을 통해 GMM을 학습시켜보자. 그리고 마지막으로 GMM을 이용한 clustering도 알아보자.
GMM(Gaussian Mixture Model)
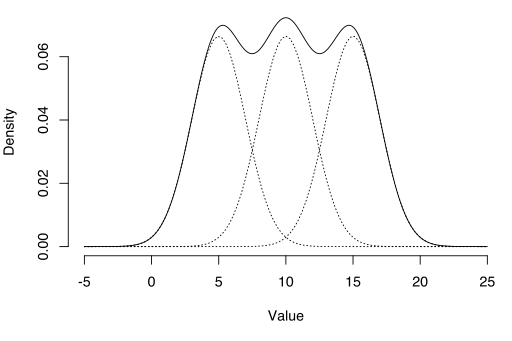
gaussian distribution의 선형결합은 아주 복잡한 밀도도 표현할 수 있다. K개의 gaussian density의 superposition은 아래와 같이 formal하게 표현할 수 있다.
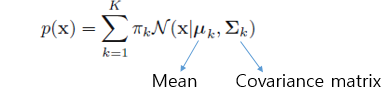
각각의 normal distribution은 아래와 같다.
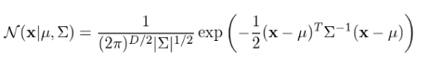
이를 gaussian의 mixture라고 부른다. 각각의 gaussian density는 mixture의 component라고 불리고, 얘들 각자는 mean과 covariance matrix를 갖고있다. 여기서 πk는 mixing coefficient라고 부른다. 이는 각각의 gaussian density가 얼마만큼의 비율로 들어가는지를 뜻하고 모두 합쳐 1이 되어야한다. 혹은 가우시안 함수의 크기를 결정한다고 볼 수 있겠다.


gaussian mixture model은 아래의 세가지 parameter에 의해 결정된다. 그러므로 주어진 데이터셋에서 아래의 세가지 파라미터를 적절히 추정하는 것이 GMM을 학습시키는 것과 같다.

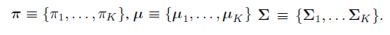
Responsibility(책임값)
앞서 가우시안 성분들을 선형으로 중첩시킨 가우시안 혼합모델을 사용하면 단일 가우시안을 이용할 때보다 더 다양한 종류의 밀도모델을 표현할 수 있다는 것을 살펴보았다. 다음파트부터 GMM의 파라미터를 찾는 것을 보일텐데, 그때 EM알고리즘의 Estep에서 사용되는 responsibility(책임값)이라는 확률값을 잠시 보고 넘어가자.
결론부터 알려주자면,

이걸 responsiblity(책임값)이라고 한다. 얘를 찾아서 긴 모험을 떠날 것이다......
먼저 데이터포인트 xn이 K개의 가우시안중에 몇번째 가우시안에서 왔는지에 대한 확률을 알고싶다고 하자. 그렇다면 아래와같이 나타낼 수 있다.


이 경우에 z는 잠재변수(latent variable)인데, x가 실제 k번째 가우시안에서 왔으면 1 그렇지 않으면 0 두가지 값만 가질 수 있다. (잠재변수는 실제 볼 수는 없지만 필요해서 가정하는 변수를 말한다) 또한 아래와 같은 표현을 할 수 있다.

이 말은 mixing coefficient πk 가 k번째 가우시안에서 오는 점을 관측할 전체확률과 같다는 것을 의미한다. πk는 가우시안함수의 크기를 나타내기 때문에 이 값이 클수록 확률이 더 높을 것이라는 의미가 있다. k개의 잠재변수 z를 모아서 벡터로 표현할 수 있다.(해당 클러스터에서만 1값을 갖는 one-hot vector)
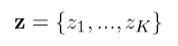
one-hot vector이기 때문에(독립, 자신이 속한 클러스터에서만1값을 취함) z의 분포를 아래와같이 쓸 수 있다.

유사하게 특정 클러스터가 정해졌을 때, x의 분포는 가우시안을 따른다..(k번째 가우시안을 따르겠지) 그러므로 아까와 동일한 논리로 조건부확률을 정의할 수 있다.

이쯤되면 지금 뭘 구하려는 건지 잊을 수도 있다. 다시한번 상기시키면 아래의 식을 구하려고 한다.

x가 나올 확률같은 경우에 처음에 정의했던 gaussian mixture 로 나타낼 수 있다.

이제 정의한 것들을 이용하여 구하고자했던 데이터포인트 xn이 K개의 가우시안중에 몇번째 가우시안에서 왔는지에 대한 확률 식을 완성해보자!!! 베이즈 정리를 이용하면,


아래의 식을 통해 책임값을 완성할 수 있다.

MLE를 이용한 GMM의 파라미터 찾기
이번 파트에서는 EM알고리즘을 이용하여 GMM의 파라미터를 찾는 방법을 알아보겠다. 여기서의 objective function은 log-likelihood이다. 얘를 maximize하는 해를 찾을 것이다.

위의 확률은 GMM파라미터가 주어졌을 때, 데이터셋을 표현할 확률을 나타내는 것으로 이를 최대화 하는 방향으로 모델의 파라미터를 학습해야할 것이다. 그러므로 각각의 파라미터에 대해 편미분을 하여 파라미터값을 추정할 수 있다. 여기서 아까 구해뒀던 책임값으로 모두 표현할 수 있게 된다.
1)mean: mean으로 편미분해서 0이되는 지점을 찾는다.
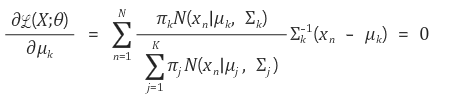


2)covariance: covariance로 편미분해서 0이되는 지점을 찾는다.

3)mixing coefficient: mixing coefficient같은 경우에는 제약조건이 있기때문에 라그랑주승수로 풀 수 있다.
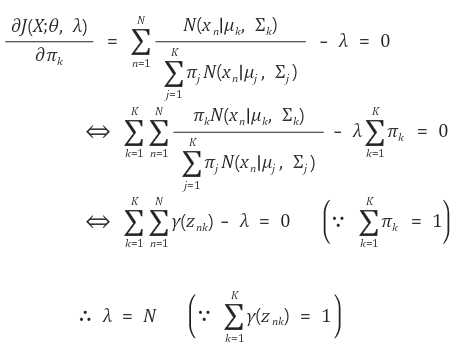

EM알고리즘을 이용한 GMM파라미터 최적화
앞선 파트에서 계산한 모든 파라미터들의 해는 나머지 값들이 고정되어 있을 때 구할 수 있다. 그러므로 여러해를 동시에 구하기 위해서는 EM알고리즘이라는 단순하고 반복적인 방식을 취할 수 있다.
- 일단 모든 파라미터를 초기화한다.
- E step: 초기 파라미터를 고정해두고 responsibility(책임값)을 구한다.
- M step: 현재 responsibility을 앞서 구한 MLE solution(세가지 파라미터의 해)에 대입하여 업데이트한다.
- log likelihood로 평가한다.

GMM을 이용한 clustering
이제 GMM을 어디에 쓰냐라고 물어볼 수 있겠다.... GMM을 이용하여 k-means clustering처럼 clustering을 할 수 있는데, 앞선 EM알고리즘에서 구했던 각각의 가우시안 분포의 평균값이 cluster center가 되게 하면 clustering을 할 수 있다. 바로 이전 포스팅에서 봤던 K-means clustering의 중요한 특징으로는 hard clustering method라는 점이다. 즉, 각 포인트를 하나의 클러스터에만 연결하게 된다. 이 접근법의 한계는 데이터포인트가 특정 클러스터와 얼마나 관련이 있는지 알려주는 불확실성 혹은 확률이 없다는 것이다. 이런 한계를 해결하기 위해 GMM을 사용해볼 수 있다.
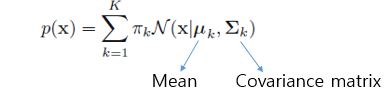

아래의 경우에는 cluster가 3개이므로 위의 식에서 K=3으로 설정하면 되겠다.

여기서 다시 책임값이 나오는데, 데이터포인트 xn이 K개의 가우시안중에 몇번째 가우시안에서 왔는지에 대한 확률 을 책임값이라고 했다. 그러므로 책임값이 가장 큰 k로 클러스터링을 할 수 있을 것이다. 그 알고리즘은 아래와 같다.

아래의 그림 K=2일때, EM알고리즘 적용을 나타낸다. 여기서 동그라미 두개는 두 가우시안의 단위표준편차 경로이고,
초록색 점들이 빨강,파랑으로 점점 칠해지는것은 확률 값을 기준으로 칠한 것이다.
b)는 Estep을 나타내고 (확률(책임값) 계산)
c)는 Mstep을 나타낸다. (평균이 옮겨감)
이를 20사이클 반복한 것이 f)이다. 여기서 알고리즘이 거의 수렴한 것을 살펴볼 수 있다.

Reference
Bishop - Pattern Recognition And Machine Learning
https://towardsdatascience.com/gaussian-mixture-models-explained-6986aaf5a95
'ML&DL > Machine Learning' 카테고리의 다른 글
| MAP와 Regularization(Ridge/Lasso)의 관계 (0) | 2025.12.11 |
|---|---|
| HMM(Hidden Markov Model, 은닉마르코프모델) 원리 (0) | 2020.06.13 |
| K-means clustering(K-평균 군집화) 원리 (0) | 2020.06.13 |
| Kernel/Kernel trick(커널과 커널트릭) (4) | 2020.06.13 |
| Regularization(정규화): Ridge regression/LASSO (0) | 2020.06.13 |



