Input의 선형조합(어떤 weight와의 곱을 다 더함)으로 output을 결정하는 많은 모델들을 살펴봤다. linear regression, logistic regression, SVM, perceptron... 더 나아가 NN에서도 weighted sum을 활용한다. SVM같이, 선형모델을 분류모델로 가정했을 때, 선형으로 완전히 분류할 수 없는 데이터분포를 만나게 될지도 모른다. 그때, soft margin SVM같은 경우는 soft margin을 두어, 즉 어느정도의 오류는 허용하는 형태로 분류를 했다. 그걸로는 좀 모자르다고 생각할 수 있다. 그럼 어떻게 더 잘 분류할 수 있을지 고민해보게 된다.
linear하게 separable하지 않은 애들을 좀 구불구불한 decision boundary로 분류할 수 있다면 얼마나 좋을까? input data를 어떤 mapping function을 이용해 높은 차원으로 올려줄 수 있다. 올려준 차원에서는 선으로 분류될 수 있게되는데, 그럼 원래 input의 dimension에서 구불구불하게 분류해낸 격이 된다. 근데, 이런 mapping과정에 내적까지 하면 연산량이 너무 많아진다. 그때 이용하는게 kernel trick(커널트릭)이다.
그럼, 고차원으로 매핑하는 과정에 대해 이해해보고, 내적연산과 매핑함수를 합치는 방법인 kernel trick에 대해 알아보자. (사실 kernel함수는 밀도추정에도 쓰이지만 이에 대해선 나중에 기회가 되면 포스팅해보는 걸로...)
더 높은 차원으로의 mapping function
이해하기 쉬운 예제를 통해 감을 좀 잡아보자. 1-D data가 아래와 같이 존재한다고 하자.
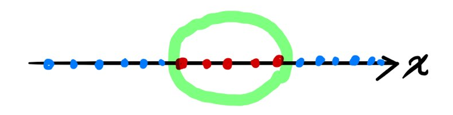
이 데이터는 선으로 딱 잘라서 구분할 수가 없이 중간에 빨간색이 낑겨있는 것을 알 수 있다. 여기서 다른 dimension을 추가해보자.
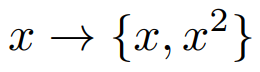
1차원 데이터를 2차원 데이터로 mapping했다. 그러면 2차원 평면에 데이터를 나타낼 수 있고 아래와 같이 선으로 둘을 분리할 수 있게 되었다.
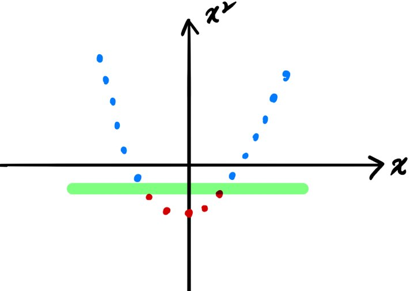
이번엔 2차원 data를 3차원으로 넘겨보자. 그리고 이는 수식으로도 한번 정리해보도록 하자. 2-D data가 아래와 같이 존재한다고 하자.
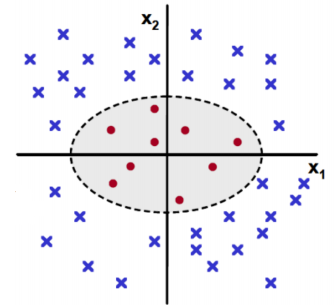
얘도 보면 빨간점이 중간에 기분나쁘게 뭉쳐있어서 선으로는 절대 분리해낼 수 없는 상황이다. 이때, 3개의 기저를 가진 3차원으로 mapping하는 식을 아래와 같이 잡았다고 하자. 이 변환을 mapping function이라고 부른다.


z의 각 성분이 z1,z2,z3축을 형성하게 되고, 아래와 같이 선형으로 분리해낼 수 있다고 한다.

근데 이런 mapping function을 SVM에 적용한다고 생각해보자. Dual표현으로 SVM식을 쓰면?
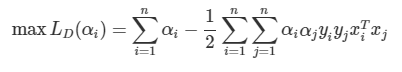
여기서 mapping함수를 x에 적용하면 어떻게 될까?
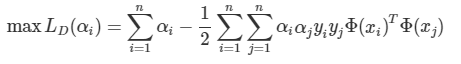
mapping함수를 이용했더니 고차원으로의 연산에 더불어 또 내적까지 해야한다. 이게 싫어서 이용하는 것이 이제 kernel이 되겠다.
Kernel trick(커널트릭)과 Kernel(커널)
아까 수식으로 돌아가서 1)고차원 mapping 2)내적 두가지를 한번에 하고싶은게 바로 kernel이다.


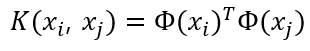
위의 노란형광펜을 친 부분을 합쳐서 이제 kernel(커널)이라고 할 것이다. 이렇게 SVM에서 kernel함수를 이용한 trick을 한다고 kernel trick이라고 한다. mapping함수와 커널의 차원을 한번 살펴보자.

i와 j의 커널값을 구하면 스칼라로 나오게된다. 커널로 행렬을 만들어보자....
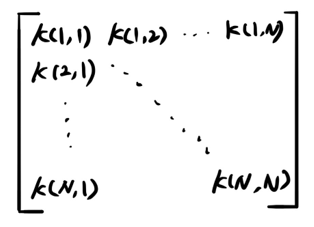
커널함수는 밀도추정에도 쓰인다. 고로 대칭이고 non-negative를 이해할 수 있을 것이다. kernel행렬을 만들어보면 i와 j가 같을 때, 값이 0이상 이어야할 것(semi-defined matrix)이고 대칭행렬이어야 할 것이다.

커널트릭을 perceptron에도 쓸 수 있어 kernelized perceptron식을 남겨본다.

Kernel(커널)로 쓰이는 함수
이제 kernel로 쓰이는 함수들을 좀 살펴보도록 하자. (위키피디아를 보다가 번역이 너무 귀여워서 첨부..)

인기있는 커널들^_^
1)Polynomial kernel(다항식커널)
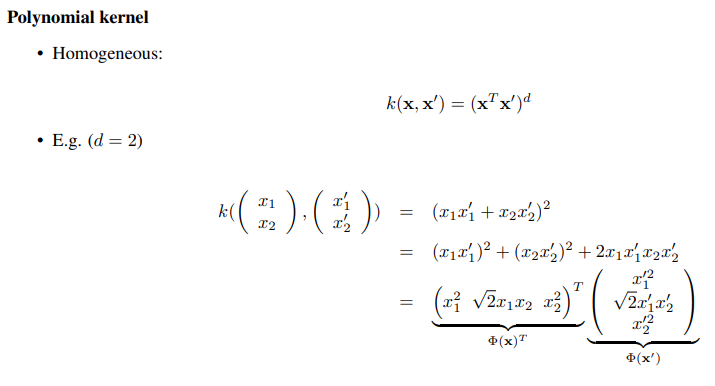
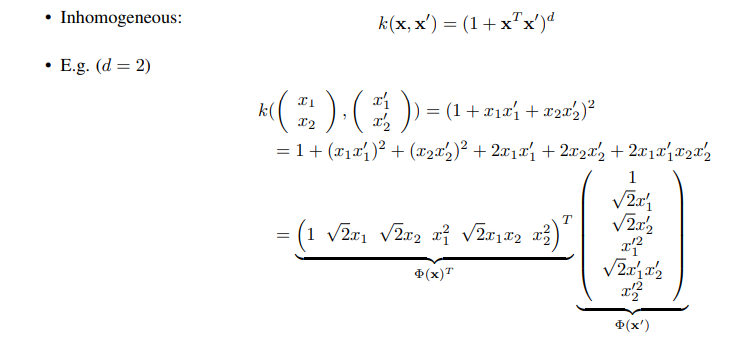
2)Gaussian kernel(가우시안 커널)

(+여러 커널들 요약정리본)
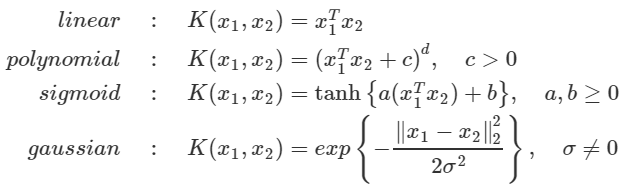
Reference
https://ratsgo.github.io/machine%20learning/2017/05/30/SVM3/
'ML&DL > Machine Learning' 카테고리의 다른 글
| GMM(Gaussian Mixture Model,가우시안 혼합모델) 원리 (4) | 2020.06.13 |
|---|---|
| K-means clustering(K-평균 군집화) 원리 (0) | 2020.06.13 |
| Regularization(정규화): Ridge regression/LASSO (0) | 2020.06.13 |
| Linear regression/Logistic regression 원리 (0) | 2020.06.13 |
| Naive bayes classifier(나이브 베이즈 분류기) 원리 (0) | 2020.06.13 |



