이전 포스팅에서는 "데이터의 노이즈가 가우시안 분포를 따른다"는 가정하에, MLE(최대 우도 추정)가 우리가 흔히 쓰는 최소 제곱법(Least Square)과 수학적으로 동일하다는 것을 증명했다.
$$
\text{MLE} \approx \text{Minimize MSE (Mean Squared Error)}
$$
하지만 MLE(또는 최소 제곱법)에는 치명적인 단점이 하나 있다. 바로 과적합(Overfitting)이다. 모델이 학습 데이터에 너무 과도하게 맞춰진 나머지, 파라미터(Weight) 값들이 비정상적으로 커지거나 불안정해지는 현상이다. 머신러닝에서는 이를 막기 위해 손실 함수(Loss Function)에 규제항(Regularization Term)을 추가한다.
$$
\text{Loss} = \text{Error} + \lambda (\text{Penalty})
$$
그런데 이 '패널티(Penalty)'는 도대체 어디서 튀어나온 것일까? 단순히 "값이 너무 커지면 안 되니까 강제로 줄이자"라는 직관에서 나온 것일까? 놀랍게도, 베이지안 관점의 MAP(Maximum A Posteriori)를 들여다보면 이 규제항의 수학적 정체를 정확히 알 수 있다.
MAP의 재발견: Posterior를 최대화하라
우리의 목표는 사후 확률(Posterior)을 최대화하는 파라미터 \( w \)를 찾는 것이다. 베이즈 정리에 의해 식은 다음과 같다.
$$
\log P(w|D) \propto \underbrace{\log P(D|w)}_{\text{Likelihood}} + \underbrace{\log P(w)}_{\text{Prior}}
$$
이 식을 최대화(Maximize)하는 것은, 부호를 반대로 뒤집은 식을 최소화(Minimize)하는 것과 같다.
$$
\text{Loss}_{MAP} = \underbrace{-\log P(D|w)}_{\text{Error Term}} + \underbrace{-\log P(w)}_{\text{Regularization Term}}
$$
- 첫 번째 항 (\( -\log P(D|w) \)): 지난 시간에 보았듯, 노이즈가 가우시안이라면 MLE term은 MSE(오차 제곱 합)가 된다.
- 두 번째 항 (\( -\log P(w) \)): 바로 이것이 규제항(Regularization)이 된다!
즉, 우리가 손실 함수 뒤에 붙이는 규제항은 사실 "파라미터 \( w \)에 대한 사전 믿음(Prior Belief)"을 수식으로 표현한 것이다.
Ridge Regression (L2 규제)와 가우시안 사전확률
우리가 가장 흔히 사용하는 릿지 회귀(Ridge Regression)는 오차항에 가중치의 제곱합(\( \sum w^2 \))을 더해서 최소화한다.
$$
\text{Loss}_{Ridge} = \text{MSE} + \lambda \sum w^2
$$
이 식은 베이지안 관점에서 "가중치 \( w \)가 가우시안 분포(정규분포)를 따른다"고 가정한 MAP와 같다. 우리의 사전 믿음(Prior)이 "파라미터 \( w \)는 0을 중심으로 하는 정규분포를 따른다"는 것이라고 해보자. (대부분의 가중치는 0 근처의 작은 값일 것이라는 믿음)
$$
P(w) \propto \exp \left( - \frac{w^2}{2\sigma^2} \right)
$$
이 식에 로그를 취하고 마이너스를 붙여보자 (MAP 식의 두 번째 항).
$$
-\log P(w) \propto - \left( - \frac{w^2}{2\sigma^2} \right) = \frac{1}{2\sigma^2} w^2
$$
상수 \( \frac{1}{2\sigma^2} \)를 \( \lambda \)로 치환하면, 우리가 아는 L2 규제항(\( \lambda w^2 \))이 툭 튀어나온다.
결론: Ridge Regression은 "파라미터의 사전 분포가 가우시안(Gaussian)이다"라고 가정한 MAP 추정이다.
Lasso Regression (L1 규제)와 라플라스 사전확률
변수 선택(Feature Selection) 효과가 있는 라쏘 회귀(Lasso Regression)는 오차항에 가중치의 절댓값 합(\( \sum |w| \))을 더한다.
$$
\text{Loss}_{Lasso} = \text{MSE} + \lambda \sum |w|
$$
이 식은 베이지안 관점에서 "가중치 \( w \)가 라플라스 분포(Laplace Distribution)를 따른다"고 가정한 MAP와 같다. 우리의 사전 믿음이 "파라미터 \( w \)는 0일 확률이 매우 높고, 0에서 멀어질수록 급격히 확률이 줄어든다"는 것이라고 해보자. 이는 뾰족한 산 모양을 가진 라플라스 분포로 표현된다.
$$
P(w) \propto \exp \left( - \frac{|w|}{b} \right)
$$
마찬가지로 로그를 취하고 마이너스를 붙여보자.
$$
-\log P(w) \propto - \left( - \frac{|w|}{b} \right) = \frac{1}{b} |w|
$$
상수 \( \frac{1}{b} \)를 \( \lambda \)로 치환하면, 이것이 바로 L1 규제항(\( \lambda |w| \))이다.
결론: Lasso Regression은 "파라미터의 사전 분포가 라플라스(Laplace)이다"라고 가정한 MAP 추정이다.
한눈에 정리: 분포와 규제의 관계
직관적인 이해를 위해 표와 그림으로 정리해 보았다.
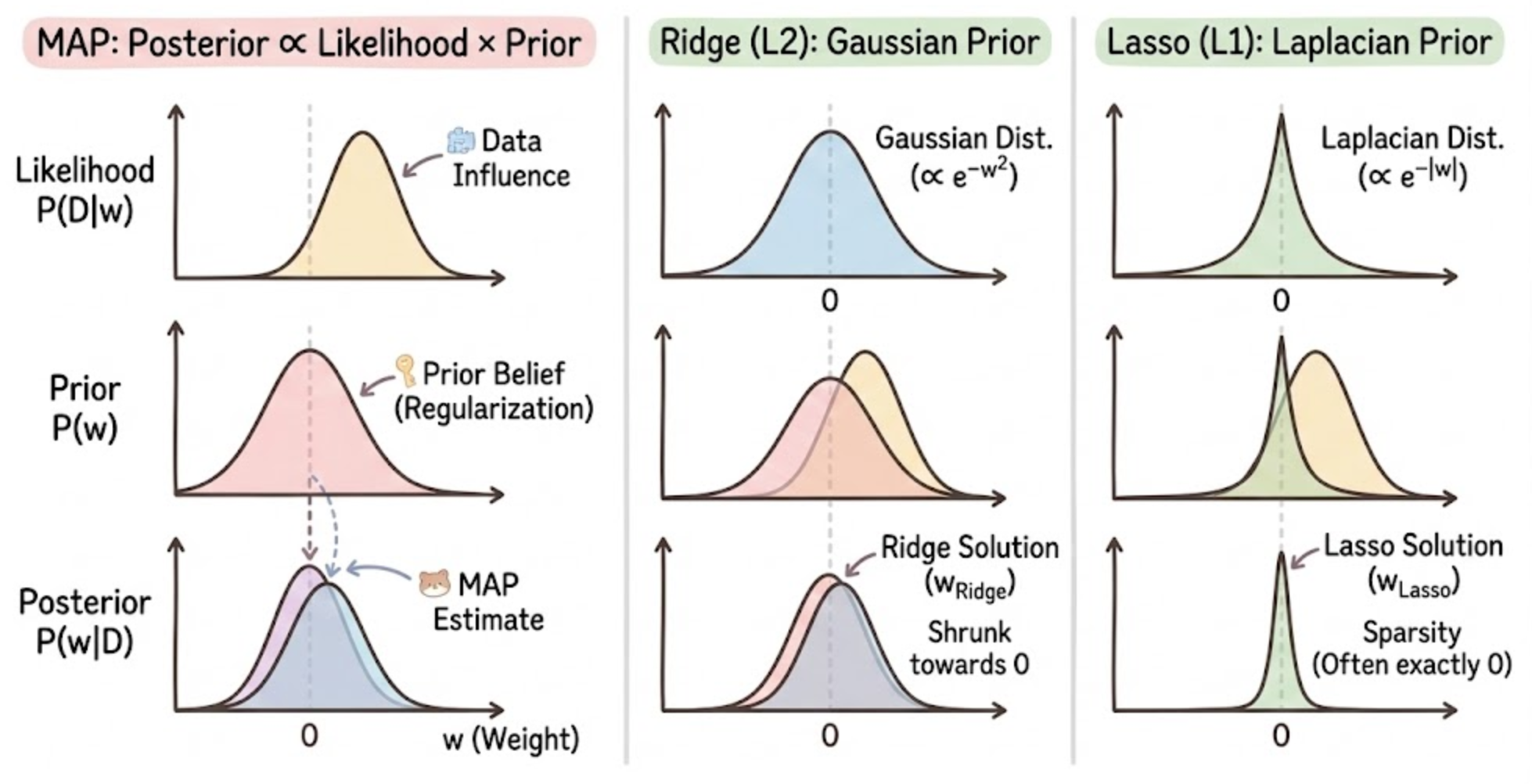
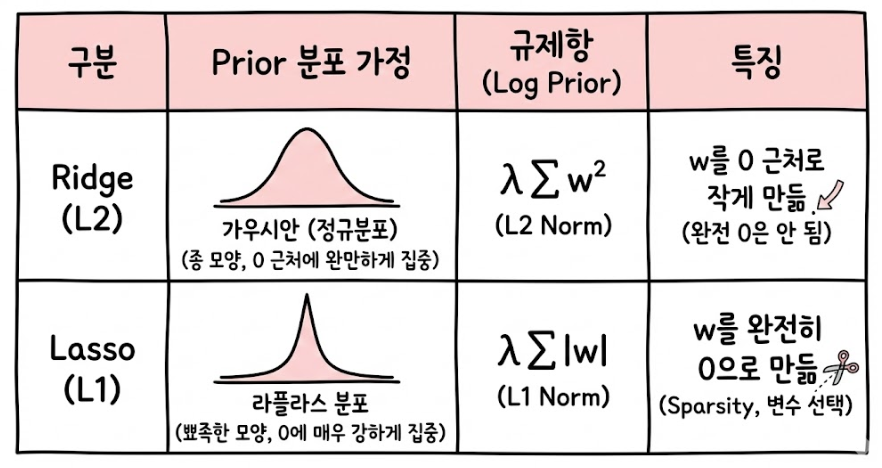
- 가우시안(Ridge): 0에서 부드럽게 떨어짐 → 가중치를 부드럽게 0으로 당김.
- 라플라스(Lasso): 0에서 뾰족함 → 가중치를 강력하게 0으로 만듦. (feature selection효과!)
마치며
머신러닝 모델을 학습시킬 때 무심코 추가했던 penalty='l2' 혹은 lambda 값. 그것은 단순히 과적합을 막기 위한 기술적인 도구를 넘어, "나는 세상이(파라미터가) 이렇게 생겼을 거라고 믿어"라는 우리의 사전 지식(Prior Belief)을 모델에 주입하는 행위였다.
- MLE: 오직 데이터만 믿는다. (Overfitting 위험)
- MAP (Ridge/Lasso): 데이터와 나의 믿음(Prior)을 함께 고려한다. (Regularization 효과)
이로써 베이지안 관점에서의 학습(Learning) 시리즈, MLE부터 MAP, 그리고 Regularization까지의 연결 고리가 완성되었다.
Reference
Christopher Bishop, Pattern Recognition and Machine Learning
Kevin Murphy, Machine Learning: A Probabilistic Perspective
'ML&DL > Machine Learning' 카테고리의 다른 글
| HMM(Hidden Markov Model, 은닉마르코프모델) 원리 (0) | 2020.06.13 |
|---|---|
| GMM(Gaussian Mixture Model,가우시안 혼합모델) 원리 (4) | 2020.06.13 |
| K-means clustering(K-평균 군집화) 원리 (0) | 2020.06.13 |
| Kernel/Kernel trick(커널과 커널트릭) (4) | 2020.06.13 |
| Regularization(정규화): Ridge regression/LASSO (0) | 2020.06.13 |



